1 Introduction
Minkowski problem is one of the cornerstones of the Brunn-Minkowski theory. In the 1890s, Minkowski proposed the Minkowski problem and solved the discrete case. The Minkowski problem was completely solved by Alexsandrov and Fenchel and Jessen.
The
$L_{p}$
Minkowski problem is a part of
$L_{p}$
Brunn-Minkowski theory. Lutwak [Reference Lutwak19] proposed the
$L_{p}$
Minkowski problem and solved the even
$L_{p}$
Minkowski problem for
$p>1$
, but
$p \ne n$
. After that, the
$L_{p}$
Minkowski problem and related researches can be found in [Reference Bianchi, Böröczky, Colesanti and Yang1, Reference Böröczky, Lutwak, Yang and Zhang2, Reference Böröczky and Trinh3, Reference Chen, Li and Zhu4, Reference Chou and Wang5, Reference Guan and Xia9, Reference Huang, Lutwak, Yang and Zhang15, Reference Huang and Zhao16, Reference Hug, Lutwak, Yang and Zhang17].
The Orlicz Brunn-Minkowski theory originated from the work of Lutwak, Yang, and Zhang in 2010 [Reference Lutwak, Yang and Zhang21]. The development of the Orlicz Brunn-Minkowski theory can be found in [Reference Gardner, Hu and Weil6, Reference Haberl, Lutwak, Yang and Zhang11, Reference Xi, Jin and Leng23]. Harbel, Lutwak, Yang, and Zhang [Reference Haberl, Lutwak, Yang and Zhang11] first proposed the Orlicz Minkowski problem, which is the extension of the
$L_{p}$
Minkowski problem, and solved the even Orlicz Minkowski problem under some suitable conditions on
$\varphi $
. The existence of the Orlicz Minkowski problem without assuming that
$\mu $
is the even measure was solved by Huang and He [Reference Huang and He14], but needing more conditions on
$\varphi $
, the
$L_{p}$
Minkowski problem for
$p>1$
is a special case of this result. For
${0<p<1}$
, Wu, Xi, and Leng [Reference Wu, Xi and Leng22] solved the existence of the discrete Orlicz Minkowski problem. The Orlicz Minkowski problem and related researches can be found in [Reference Gardner, Hug, Weil, Xing and Ye7, Reference Gardner, Hug, Xing and Ye8, Reference Xie25, Reference Xie26].
Recently, a new family of geometric measures was introduced by Lutwak, Xi, Yang, and Zhang [Reference Lutwak, Xi, Yang and Zhang20] through the study of a variational formula with respect to integral geometric invariants of convex bodies called chord integrals. Minkowski problems associated with chord measures were posed in [Reference Lutwak, Xi, Yang and Zhang20].
Let
$\mathcal {K} ^{n } $
be the collection of convex bodies (compact convex sets with nonempty interior) in
$\mathbb R^{n}$
. For
$K\in \mathcal {K} ^{n}$
, the chord integral
$I_{q}(K) $
of K is defined as follows:
$$ \begin{align*}I_{q}(K)=\int\limits_{\mathcal{L}^{n}}\left | K\cap \ell \right |^{q} \mathrm{d}\ell,\quad q\ge 0,\end{align*} $$
where
$\left | K\cap \ell \right |$
denotes the length of the chord
$ K\cap \ell $
, and the integration is with respect to the Haar measure on the Grassmannian
$\mathcal {L}^{n}$
of lines in
$\mathbb R^{n}$
.
Chord integrals contain volume
$V(K)$
and surface area
$S(K)$
as two important special cases:
$$ \begin{align*}I_{1}(K)=V(K),\quad I_{0} (K)=\frac{\omega _{n-1} }{n\omega _{n} } S(K),\quad I_{n+1} (K)=\frac{n+1 }{\omega _{n} }V (K)^{2} , \end{align*} $$
where
$\omega _{n}$
is the volume enclosed by the unit sphere
$\mathbb {S}^{n-1} $
.
The differential of
$ I_{q}(K)$
defines a finite Borel measure
$F_{q} (K, \cdot )$
on
$\mathbb {S}^{n-1} $
. Precisely, for convex bodies K and L in
$\mathbb R^{n}$
, Lutwak, Xi, Yang, and Zhang [Reference Lutwak, Xi, Yang and Zhang20] obtained that
$$ \begin{align} \frac{\mathrm{d}}{\mathrm{d} t} \bigg|_{t=0^{+}} I_{q}(K+tL) =\int\limits_{\mathbb{S}^{n-1} }h_{L}(v)\mathrm{d}F_{q}(K,v),\quad q\ge 0, \end{align} $$
where
$F_{q} (K, \cdot \, )$
is called the qth chord measure of K, and
$h_{L}$
is the support function of L. The cases of
$q=0,1$
of this formula are classical, which are the variational formulas of surface area and volume,
$$ \begin{align*}F_{0}(K,\cdot\, ) =\frac{(n-1)\omega_{n-1}}{n\omega_{n}} S_{n-2}(K,\cdot ), \quad F_{1}(K,\cdot\, ) = S_{n-1}(K,\cdot\, ) .\end{align*} $$
Here,
$S_{n-2}(K,\cdot \, )$
and
$S_{n-1}(K,\cdot \, )$
are the
$({n}-2)$
th order and
$(n-1)$
th order area measure of K, respectively.
Based on the definition of chord measure, the corresponding chord Minkowski problem was proposed. The solution to the chord Minkowski problem as
$q>0$
was given in [Reference Lutwak, Xi, Yang and Zhang20].
The
$L_{p}$
version of the chord measure was also introduced in [Reference Lutwak, Xi, Yang and Zhang20]; it can be extended from the
$L_{p}$
surface area measure. Correspondingly, the
$L_{p}$
chord Minkowski problem was considered. Xi, Yang, Zhang, and Zhao [Reference Xi, Yang, Zhang and Zhao24] solved the
$L_{p}$
chord Minkowski problem when
$p>1$
,
$q>1$
and the symmetric case of
$0<p<1$
via the variational method. Guo, Xi, and Zhao [Reference Guo, Xi and Zhao10] solved the
$L_{p}$
chord Minkowski problem for
$0\le p< 1$
without symmetry assumptions. Li [Reference Li18] treated the discrete
$L_{p}$
chord Minkowski problem in the condition of
$p<0$
and
$q>0$
, as for general Borel measure. Li also gave a proof but need
$-n<p<0$
and
$1<q<n+1$
. Hu, Huang, and Lu [Reference Hu, Huang and Lu12] used flow methods to get regularity of the chord log-Minkowski problem of
$p=0$
. On the side, Hu, Huang, Lu, and Wang [Reference Hu, Huang, Lu and Wang13] also found the smooth origin-symmetric solution for the
$L_{p}$
chord Minkowski problem in the case of
$\left \{ p> 0,q> 3 \right \} \cup \left \{ -n<p<0, 3<q<n+1 \right \} $
by using the same flow as in [Reference Hu, Huang and Lu12].
The more generalized Orlicz chord Minkowski problem was stated in [Reference Zhao and Zhao27] by the following form:
The Orlicz chord Minkowski problem: Suppose
$\varphi :\left ( 0,\infty \right ) \longrightarrow \left ( 0,\infty \right )$
is a continuous function. If
$\mu $
is a finite Borel measure on
$\mathbb {S}^{n-1}$
which is not concentrated on a great subsphere of
$\mathbb {S}^{n-1}$
, what are the necessary and sufficient conditions on
$\mu $
such that there is a convex body
$K\in \mathcal {K}_{o}^{n}$
and a positive constant c such that
$$ \begin{align*}\mathrm{d}\mu =c\varphi \left ( h_{K} \right ) \mathrm{d}F_{q} \left ( K,\cdot \, \right ) ?\end{align*} $$
Due to the lack of homogeneity, the solution to the Orlicz chord Minkowski problem exists as a constant.
In this paper, we consider the existence of the discrete Orlicz chord Minkowski problem, which is an extension of the discrete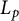
$L_{p}$
chord Minkowski problem for
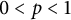$0<p<1$
[Reference Guo, Xi and Zhao10]. Our main results can be formulated as follows:
Theorem 1.1 Let
$q>0$
.
$\mu =\sum _{i=1}^{N} \alpha _{i}\delta _{v_{i}} $
for some
$\alpha _{i}>0$
, and unit vectors
$v_{1},\dots ,v_{N}\in \mathbb {S}^{n-1}$
are not contained in any closed hemisphere, where
$\delta _{v_{i}}$
is Kronecker delta. Let
$\mathcal {P}\left ( v_{1},\dots ,v_{N} \right )=\left \{ P\left ( z \right ): z\in \mathbb {R } ^{N}\;such\:that\: P\left ( z \right )\in \mathcal {K}^{n} \right \}$
. Suppose
$\varphi :(0,\infty )\to (0,\infty )$
is differentiable and strictly increasing, and
$\varphi (s)$
tends to
$0$
as
$s\to 0^{+}$
such that
$\phi (t)=\int _{0}^{t}\frac {1}{\varphi (s)}\mathrm {d}s$
exists for every positive t. Then, there exists a polytope
$P\in \mathcal {P}(v_{1},\dots ,v_{N})$
containing the origin in its interior and
$c>0$
such that
$$ \begin{align*}c\varphi(h_{P})dF_{q}(P,\cdot)=d\mu.\end{align*} $$
When
$\varphi \left ( t \right )=t^{1-p}$
for
$0<p<1$
, Theorem 1.1 is reduced to Theorem 4.6 of [Reference Guo, Xi and Zhao10]. When
$q=1$
, Theorem 1.1 is reduced to Theorem 1.2 of [Reference Wu, Xi and Leng22].
The paper is organized as follows: In Section 2, we present some notations and basic facts we shall use throughout. The proof of Theorem 1.1 is presented in Section 3.
2 preliminaries
In this section, we present some notations we shall use throughout.
2.1 Basics of convex bodies
Let
$\mathbb R^{n}$
be n-dimensional Euclidean space. The standard inner product of the vectors x,
$y\in \mathbb R^{n}$
is denoted by
$x\cdot y$
. We write
$\mathbb {S}^{n-1}=\left \{ x\in \mathbb R^{n}: x\cdot x=1 \right \} $
for the boundary of the Euclidean unit ball B in
$\mathbb R^{n}$
.
A convex body is a compact convex subset of
$\mathbb R^{n}$
with a nonempty interior. The set of convex bodies in
$\mathbb R^{n}$
is denoted by
$\mathcal {K}^{n}$
, and the set of convex bodies in
$\mathbb R^{n}$
containing the origin in their interiors is denoted by
$\mathcal {K }_{o}^{n}$
.
A compact convex set
$K\subset \mathbb R^{n} $
is uniquely determined by its support function
$h_{K} : \mathbb R^{n}\to \mathbb R, $
where
$$ \begin{align*}h_{K}\left ( x \right ) =\max_{} \left \{ x\cdot y:y\in K \right \} ,\quad x\in \mathbb R^{n}.\end{align*} $$
It is trivial that for the support function of the dilate
$cK=\left \{ cx:x\in K \right \} $
of a compact convex set K, we have
$$ \begin{align*}h_{cK}=ch_{K},\quad c>0.\end{align*} $$
Note that support functions are positively homogeneous of degree 1 and subadditive. It follows immediately from the definition of support functions that for compact convex K,
$L\subset \mathbb R^{n}, $
$$ \begin{align*}K\subseteq L\quad \Longleftrightarrow \quad h_{K} \le h_{L} .\end{align*} $$
Let
$K\in \mathcal {K}^{n}$
and
$x\in \mathbb {R}^{n}$
. The radial function of K with respect to x, denoted by
$\rho _{K,x}(u):\mathbb {S}^{n-1}\to \mathbb {R}$
, can be written as
$$ \begin{align*}\rho_{K,x}(u)=\max\left\{t:tu+x\in K\right\}.\end{align*} $$
It is simple to see that when
$x\in \mathrm{int}K$
, we have that
$\rho _{K,x}$
is a positive continuous function on
$\mathbb {S}^{n-1}$
. For simplicity, we write
$\rho _{K}=\rho _{K,o}.$
The Hausdorff distance
$d_{H}(K,L)$
of
$K,L\in \mathcal {K}^{n}$
is defined by
$$ \begin{align*}d_{H}(K,L):=\max_{u\in \mathbb{S}^{n-1}}\left | h_{K}(u)-h_{L}(u) \right |.\end{align*} $$
The set
$ \mathcal {K }^{n}$
will be viewed as equipped with the Hausdorff metric. If there exists a sequence
${K_{i}}$
of convex bodies in
$ \mathcal {K }^{n}$
and a convex body
$K\in \mathcal {K }^{n}$
, we say that
$\lim _{i \to \infty } K_{i}=K$
provided
$$ \begin{align*}\left \| h_{K_{i}}-h_{K} \right \| _{\infty }\to 0.\end{align*} $$
Suppose
$\Omega $
is a compact subset of
$\mathbb {S}^{n-1}$
that is not concentrated in any closed hemisphere. The set of continuous functions on
$\Omega $
will be denoted by
$C(\Omega )$
. For
$h\in C^{+}\left ( \Omega \right ) $
, the Wulff-shape
$\left [ h \right ]$
is a compact convex set defined by
$$ \begin{align*}\left [ h \right ] =\left \{ x\in \mathbb{R} ^{n}:x\cdot v\le h\left ( v \right ), \forall v\in \Omega \right \} .\end{align*} $$
It is simple to see that
$$ \begin{align} h_{\left [ h \right ] } \left ( v \right ) \le h\left ( v \right ). \end{align} $$
We shall frequently use the fact that if
$h_{i}\in C(\Omega )$
convergence to
$h\in C(\Omega )$
uniformly, then the
$[h_{i}]\to [h]$
in Hausdorff metric.
A useful fact is that, when
$\left [ h \right ]\in \mathcal {K} ^{n} $
, the support of
$S_{n-1}\left ( \left [ h \right ], \cdot \, \right ) $
must be contained in
$\Omega $
. In particular, let
$v_{1},\dots v_{N} \left ( N \ge n+1 \right ) $
be unit vectors that are not contained in any closed hemisphere, and let
$\Omega =\left \{ v_{1},\dots ,v_{N} \right \} $
. For
$z=\left ( z_{1},\dots ,z_{N} \right ) \in \mathbb {R}^{N} $
, we write
$$ \begin{align*}\left [ z \right ] =P\left ( z \right ) =\bigcap_{i=1}^{N}\left \{ x\in \mathbb{R}^{n}: x\cdot v_{i}\le z_{i} \right \}.\end{align*} $$
Define
$\mathcal {P}\left ( v_{1},\dots ,v_{N} \right )$
by
$$ \begin{align*}\mathcal{P}\left ( v_{1},\dots ,v_{N} \right )=\left \{ P\left ( z \right ): z\in \mathbb{R } ^{N}\quad \mathrm{such\,that}\, P\left ( z \right )\in \mathcal{K}^{n} \right \}.\end{align*} $$
2.2 Chord integral and chord measure
Let
$K\in \mathcal {K}^{n}$
. For
$z\in \mathrm {int}K$
and
$q\in \mathbb {R}$
, the qth dual quermassintegral
$\widetilde {V}_{q}(K,z)$
of K with respect to z is
$$ \begin{align*}\widetilde{V}_{q}(K,z)=\frac{1}{n}\int\limits_{\mathbb{S}^{n-1}}\rho_{K,z}^{q}(u)\mathrm{d}u,\end{align*} $$
where
$\rho _{K,z}(u)=\max \{\lambda>0:z+\lambda u\in K\}$
is the radial function of K with respect to z. When z is the origin, it reduces to the radial function
$\rho _{K}(u)$
. When
$z\in \partial K$
,
$\widetilde {V}_{q}(K,z)$
is defined in the way that the integral is only over those
$u\in \mathbb {S}^{n-1}$
such that
$\rho _{K,z}(u)>0.$
In other words,
$$ \begin{align*}\widetilde{V}_{q}(K,z)=\frac{1}{n}\int\limits_{\rho_{K,z}(u)>0}\rho_{K,z}^{q}(u)\mathrm{d}u,\quad \mathrm{whenever}\, z\in \partial K.\end{align*} $$
The integrals of dual quermassintegrals with respect to
$z\in K$
naturally give rise to translation invariant quantities. These are known as chord integrals in integral geometry. For
$K\in \mathcal {K} ^{n}$
, the chord integral
$I_{q}(K) $
of K is defined as follows:
$$ \begin{align*}I_{q}(K)=\int\limits_{\mathcal{L}^{n}}\left | K\cap \ell \right |^{q} \mathrm{d}\ell,\quad q\ge 0,\end{align*} $$
where
$\left | K\cap \ell \right |$
denotes the length of the chord
$ K\cap \ell $
, and the integration is with respect to the Haar measure on the Grassmannian
$\mathcal {L}^{n}$
of lines in
$\mathbb R^{n}$
.
For
$q>0$
, the chord integral can be written as the integral of dual quermassintegrals in
$z\in K$
:
$$ \begin{align*}I_{q}(K)=\frac{q}{\omega_{n}}\int\limits_{K}\widetilde{V}_{q-1}(K,z)\mathrm{d}z.\end{align*} $$
In analysis, chord integral can be recognized as the Riesz potential: for each
$q>1$
, we have
$$ \begin{align} I_{q}(K)=\frac{q(q-1)}{n\omega_{n}}\int\limits_{K}\int\limits_{K}\frac{1}{\left | x-z \right | ^{n-q+1}}\mathrm{d}x \mathrm{d}z. \end{align} $$
An elementary property of the functional
$I_{q}$
is its homogeneity. If
$K \in \mathcal {K}^{n}$
and
${q \ge 0}$
, then
$$ \begin{align*}I_{q}\left ( tK \right ) = t^{n+q-1}I_{q}\left ( K \right )\end{align*} $$
for
$t>0$
. By compactness of K, it is simple to see that the chord integral
$I_{q}\left ( K \right )$
is finite whenever
$q>0$
.
Let
$K\in \mathcal {K}^{n}$
and
$q>0.$
the chord measure
$F_{q}(K,\cdot \, )$
is a finite Borel measure on
$\mathbb {S}^{n-1}$
given by
$$ \begin{align*}F_{q}(K,\eta)=\frac{2q}{\omega_{n}}\int\limits_{\nu_{K}^{-1}(\eta)}\widetilde{V}_{q-1}(K,z)\mathrm{d}\mathcal{H}^{n-1}(z),\quad \mathrm{for\, each\, Borel\,set}\,\eta\subset \mathbb{S}^{n-1},\end{align*} $$
where
$\nu _{K}:\partial K\to \mathbb {S}^{n-1}$
is the Gauss map that takes boundary points of K to their corresponding outer unit normals. Note that by convexity of K, its Gauss map
$\nu _{K}$
is almost everywhere defined on
$\partial K$
with respect to the
$(n-1)$
-dimensional Hausdorff measure.
The significance of the chord measure
$F_{q}(K,\cdot \, )$
is that it comes from differentiating, in a certain sense, the chord integral
$I_{q}$
; see [Reference Lutwak, Xi, Yang and Zhang20]. It is simple to see that the chord measure
$F_{q}(K,\cdot \, )$
is absolutely continuous with respect to the surface area measure
$S_{n-1}\left ( K,\cdot \, \right )$
. In particular, for each
$P\in \mathcal {P}\left ( v_{1},\dots ,v_{N} \right )$
, we have that the chord measure
$F_{q} \left ( P, \cdot \,\right )$
is supported entirely on
$\left \{ v_{1},\dots ,v_{N} \right \}$
. It was shown in Theorem 4.3 of [Reference Lutwak, Xi, Yang and Zhang20] that
$$ \begin{align*}I_{q}(K)=\frac{1}{n+q-1 }\int\limits_{\mathbb{S}^{n-1}}h_{K}\left ( v \right ) \mathrm{d}F_{q}\left ( K, v \right ).\end{align*} $$
The following lemma shows the variational formula of the chord integral.
Lemma 2.1 [Reference Lutwak, Xi, Yang and Zhang20]
Let
$q>0$
and
$\Omega $
be a compact subset of
$\mathbb {S}^{n-1}$
that is not concentrated on any closed hemisphere. Suppose that
$g : \Omega \to \mathbb R$
is continuous and
$h_{t} : \Omega \to \left ( 0,\infty \right ) $
is a family of continuous functions given as follows:
$$ \begin{align*}h_{t}=h_{0}+tg+o(t,\cdot\, ),\end{align*} $$
for each
$t\in (-\delta ,\delta )$
for
$\delta>0$
. Here,
$o(t,\cdot \, )\in C(\Omega )$
and
$ o(t,\cdot \, )/t$
tends to 0 uniformly on
$\Omega $
as
$t\to 0$
. Let
$K_{t}$
be the Wulff-shape generated by
$h_{t}$
and K be the Wulff-shape generated by
$h_{0}$
. Then,
$$ \begin{align*}\frac{\mathrm{d}}{\mathrm{d} t} \bigg|_{t=0} I_{q}(K_{t}) =\int\limits_{\Omega }g(v)\mathrm{d}F_{q}(K,v).\end{align*} $$
Taking
$\Omega $
to be a finite set
$\left \{ v_{1},\dots v_{N} \right \}$
, where the
$v_{i} \in \mathbb {S}^{n-1} $
are not contained entirely in any closed hemisphere, we immediately obtain the following corollary for the discrete case.
Corollary 2.2 [Reference Guo, Xi and Zhao10]
Let
$q> 0$
,
$z=\left ( z_{1},\dots ,z_{N} \right ) \in \mathbb {R}_{+}^{N} $
,
$\beta =\left ( \beta _{1},\dots ,\beta _{N} \right ) \in \mathbb {R}^{N}$
, and
$v_{1},\dots ,v_{N}$
be N unit vectors that are not contained in any closed hemisphere. For sufficiently small
$\left | t \right |$
, consider
$z\left ( t \right ) =z+t\beta>0$
and
$$ \begin{align*}P_{t}=\left [ z\left ( t \right ) \right ] =\bigcap_{i=1}^{N}\left \{ x\in \mathbb{R}^{n}: x\cdot v_{i}\le z_{i}\left ( t \right )= z_{i} +t\beta _{i} \right \} .\end{align*} $$
Then, for
$q>0$
, we have
$$ \begin{align} \frac{\mathrm{d} }{\mathrm{d} t} \bigg|_{t=0} I_{q}\left ( P_{t} \right )=\sum_{i=1}^{N}\beta _{i} F_{q} \left ( P_{0},v_{i} \right ). \end{align} $$
Chord measures inherit their translation invariance and homogeneity from chord integrals. The following lemma shows that the chord measure
$F_{q} \left ( K, \cdot \,\right )$
is weakly continuous on
$\mathcal {K}^n$
with respect to Hausdorff metric.
Lemma 2.3 [Reference Xi, Yang, Zhang and Zhao24]
Let
$q>0$
and
$K_{i}\in \mathcal {K}^{n} $
. If
$K_{i}\to K\in \mathcal {K}^{n}$
, then the chord measure
$F_{q} \left ( K_{i}, \cdot \,\right )$
converges to
$F_{q} \left ( K, \cdot \,\right )$
weakly.
3 The discrete Orlicz chord Minkowski problem
Let
$\mu $
be a finite discrete Borel measure on
$\mathbb {S}^{n-1}$
that is not concentrated in any closed hemisphere; that is,
$$ \begin{align} \mu= \sum_{i=1}^{N} \alpha_{i}\delta_{v_{i}}, \end{align} $$
for some
$\alpha _{i}>0$
and unit vectors
$v_{1},\dots ,v_{N}\in \mathbb {S}^{n-1}$
not contained in any closed hemisphere, where
$\delta _{v_{i}}$
is Kronecker delta.
Suppose
$\varphi :(0,\infty )\to (0,\infty )$
is differentiable and strictly increasing, and
$\varphi (s)$
tends to
$0$
as
$s\to 0^{+}$
such that
$\phi (t)=\int _{0}^{t}\frac {1}{\varphi (s)}\mathrm {d}s$
exists for every positive t. For any
$z=(z_{1},\dots ,z_{N})\in \mathbb {R}^{N}$
such that
$[z]$
has nonempty interior, we define
$$ \begin{align*}\Phi_{\phi,\mu}(z,\xi)=\sum_{j=1}^{N}\phi(z_{j}-\xi\cdot v_{j})\cdot\alpha_{j}\end{align*} $$
for each
$\xi \in [z]$
. When there is no confusion about what the underlying measure
$\mu $
is, we shall write
$\Phi _{\phi }=\Phi _{\phi ,\mu }$
.
In this section, we consider the following extremal problem:
$$ \begin{align*}\sup_{\xi\in[z]}\Phi_{\phi,\mu}(z,\xi).\end{align*} $$
We will show that the functional
$\Phi _{\phi ,\mu }(z,\cdot )$
is strictly concave in
$\xi \in \mathrm{int}[z]$
and that there exists a unique
$\xi _{\phi }(z)\in \mathrm{int}[z]$
such that
$$ \begin{align*}\sup_{\xi\in[z]}\Phi_{\phi,\mu}(z,\xi)=\Phi_{\phi,\mu}(z,\xi_{\phi}(z)).\end{align*} $$
Lemma 3.1 [Reference Wu, Xi and Leng22]
If
$\alpha _{1},\dots ,\alpha _{N}\in \mathbb {R}_{+}^{N}$
, the unit vectors
$v_{1},\dots ,v_{N}(N\ge n+1)$
are not contained in any closed hemisphere, and
$\phi $
is strictly concave on
$[0,\infty ).$
Suppose
$z=(z_{1},\dots ,z_{N})\in \mathbb {R}^{N}$
such that
$[z]$
has nonempty interior. Then,
$\Phi _{\phi ,\mu }(z,\cdot )$
is strictly concave in
$\xi \in [z].$
Then, we give the following lemma to show the existence and uniqueness of
$\xi _{\phi }(z).$
Lemma 3.2 [Reference Wu, Xi and Leng22]
Suppose
$\alpha _{1},\dots ,\alpha _{N}\in \mathbb {R}_{+}^{N}$
, and the unit vectors
$v_{1},\dots ,v_{N}(N\ge n+1)$
are not contained in any closed hemisphere. If
$\varphi :(0,\infty )\to (0,\infty )$
is differentiable and strictly increasing, and
$\varphi (s)$
tends to
$0$
as
$s\to 0^{+}$
such that
$\phi (t)=\int _{0}^{t}\frac {1}{\varphi (s)}\mathrm {d}s$
exists for every positive t and is unbounded as
$t\to \infty .$
Suppose
$z=(z_{1},\dots ,z_{N})\in \mathbb {R}^{N}$
such that
$[z]$
has nonempty interior. Then, there exists a unique
$\xi _{\phi }(z)\in \mathrm{int}[z]$
such that
$$ \begin{align*}\sup_{\xi\in[z]}\Phi_{\phi,\mu}(z,\xi)=\Phi_{\phi,\mu}(z,\xi_{\phi}(z)).\end{align*} $$
The following lemma shows the continuity of
$\xi _{\phi }(z)$
and
$\Phi _{\phi }(z,\xi _{\phi }(z))$
.
Lemma 3.3 [Reference Wu, Xi and Leng22]
Suppose
$\alpha _{1},\dots ,\alpha _{N}\in \mathbb {R}_{+}^{N}$
, and the unit vectors
$v_{1},\dots ,v_{N}(N\ge n+1)$
are not contained in any closed hemisphere. If
$\varphi :(0,\infty )\to (0,\infty )$
is differentiable and strictly increasing, and
$\varphi (s)$
tends to
$0$
as
$s\to 0^{+}$
such that
$\phi (t)=\int _{0}^{t}\frac {1}{\varphi (s)}\mathrm {d}s$
exists for every positive t and is unbounded as
$t\to \infty .$
Let
$z^{l}\in \mathbb {R}^{N}$
be such that
$\lim _{l \to \infty }z^{l}=z\in \mathbb {R}^{N}$
. If
$[z]$
has nonempty interior, then
$$ \begin{align*}\lim_{l \to \infty}\xi_{\phi}(z^{l})=\xi_{\phi}(z)\end{align*} $$
and
$$ \begin{align*}\lim_{l \to \infty}\Phi_{\phi}(z^{l},\xi_{\phi}(z^{l}))=\Phi_{\phi}(z,\xi_{\phi}(z)).\end{align*} $$
The next lemma shows that
$\xi _{\phi }(z)$
is a differentiable function with respect to vector addition in z.
Lemma 3.4 Let
$z=(z_{1},\dots ,z_{N})\in \mathbb {R}_{+}^{N}$
, and
$\mu $
be as given in (3.1). For each
$\beta \in \mathbb {R}^{N}$
, consider
$$ \begin{align*}z(t)=z+t\beta\end{align*} $$
for sufficiently small
$\left |t \right | $
so that
$z(t)\in \mathbb {R}_{+}^{N}$
. Denote
$\xi _{\phi }(t)=\xi _{\phi }(z(t)).$
If
$\xi _{\phi }(0)=o$
, then
$\xi _{\phi }^{'}(0)$
exists. Moreover,
$$ \begin{align} o=\sum_{j=1}^{N}\frac{1}{\varphi(z_{j})}\alpha_{j}v_{j}. \end{align} $$
Proof Since
$\xi _{\phi }(t)\in \mathrm{int}[z(t)]$
and maximizes
$$ \begin{align*}\sup_{\xi\in[z(t)]}\Phi_{\phi}(z(t),\xi),\end{align*} $$
taking the derivative in
$\xi $
shows
$$ \begin{align} o=\sum_{j=1}^{N}\frac{1}{\varphi(z_{j}(t)-\xi_{\phi}(t)\cdot v_{j})}\alpha_{j}v_{j}. \end{align} $$
In particular, at
$t=0$
, we have
$$ \begin{align*}o=\sum_{j=1}^{N}\frac{1}{\varphi(z_{j})}\alpha_{j}v_{j},\end{align*} $$
which establishes (3.2). Set
$$ \begin{align*}F_{\phi}(t,\xi)=\sum_{j=1}^{N}\frac{1}{\varphi(z_{j}(t)-\xi\cdot v_{j})}\alpha_{j}v_{j}.\end{align*} $$
Then, (3.3) simply says
$$ \begin{align*}F_{\phi}(t,\xi_{\phi}(t))=o.\end{align*} $$
By a direct computation, the Jocabian with respect to
$\xi $
of
$F_{\phi }$
at
$t=0$
and
$\xi =0$
is
$$ \begin{align*}\frac{\partial F_{\phi}}{\partial \xi } \bigg|_{(0,0)}=\sum_{j=1}^{N}\frac{\varphi^{'}(z_{j})}{\varphi^{2}(z_{j})}\alpha_{j}v_{j}\otimes v_{j}.\end{align*} $$
Since
$v_{1},\dots ,v_{N}$
span
$\mathbb {R}^{n}$
, we conclude that the Jocabian
$\frac {\partial F_{\phi }}{\partial \xi }$
is positive-definite at
$t=0$
and
$\xi =0.$
By the implicit function theorem, we conclude that
$\xi _{\phi }^{'}(0)$
exists.
For each
$q>0$
, we consider the optimization problem:
$$ \begin{align} \inf\left \{ \Phi_{\phi}(z,\xi_{\phi}(z)): z\in \mathbb{R}^{N}, I_{q}([z])=\left | \mu \right | \right \}. \end{align} $$
Lemma 3.5 Let
$q>0$
. If there exists
$z\in \mathbb {R}_{+}^{N}$
with
$\xi _{\phi }(z)=o$
and
$I_{q}([z])=\left | \mu \right | $
satisfying
$$ \begin{align*}\Phi_{\phi}(z,o)=\inf\left \{ \Phi_{\phi}(z,\xi_{\phi}(z)): z\in \mathbb{R}^{N}, I_{q}([z])=\left | \mu \right | \right \},\end{align*} $$
then there exists a polytope
$P\in \mathcal {P}(v_{1},\dots ,v_{N})$
containing the origin in its interior such that
$$ \begin{align*}c\varphi(h_{P})\mathrm{d}F_{q}(P,\cdot)=\mathrm{d}\mu,\end{align*} $$
where
$P=[z].$
Moreover, for each
$i=1,\dots ,N,$
we have
$$ \begin{align} h_{[z]}(v_{i})=z_{i}. \end{align} $$
Proof Let
$\beta \in \mathbb {R}^{N}$
be arbitrary and set
$z(t)=z+t\beta $
. For sufficiently small
$\left | t \right | $
, we have
$z(t)\in \mathbb {R}_{+}^{N}.$
Set
$$ \begin{align*}\lambda(t)=I_{q}([z(t)])^{-\frac{1}{n+q-1}}.\end{align*} $$
Note that
$\lambda (0)=1.$
By homogeneity of
$I_{q}$
, it is apparent that
$I_{q}([\lambda (t)z(t)])=1$
. By (2.3), we have
$$ \begin{align} \lambda^{'}(0)=-\frac{1}{n+q-1}\sum_{i=1}^{N}\beta_{i}F_{q}([z],v_{i}). \end{align} $$
Let
$\xi _{\phi }(t)=\xi _{\phi }(\lambda (t)z(t))=\lambda (t)\xi _{\phi }(z(t))$
and
$$ \begin{align*}\Psi _{\phi}(t)=\Phi_{\phi}(\lambda(t)z(t),\xi_{\phi}(z(t)).\end{align*} $$
By Lemma 3.4,
$\xi _{\phi }$
is differentiable at
$t=0.$
Moreover, (3.2) holds.
Since z is a minimizer, the fact that
$0=\Psi _{\phi }^{'}(0)$
shows
$$ \begin{align*}0=\lambda^{'}(0)\sum_{j=1}^{N}\frac{1}{\varphi(z_{j})}z_{j}\alpha_{j}+\sum_{i=1}^{N}\frac{1}{\varphi(z_{i})}\beta_{i}\alpha_{i}-\xi_{\phi}^{'}(0)\sum_{j=1}^{N}\frac{1}{\varphi(z_{j})}v_{j}\alpha_{j}.\end{align*} $$
$$ \begin{align*}0=-\frac{1}{n+q-1}\sum_{i=1}^{N}\beta_{i}F_{q}([z],v_{i})\sum_{j=1}^{N}\frac{1}{\varphi(z_{j})}z_{j}\alpha_{j}+\sum_{i=1}^{N}\frac{1}{\varphi(z_{i})}\beta_{i}\alpha_{i}. \end{align*} $$
Since
$\beta $
is arbitrary, we conclude that
$$ \begin{align*}\frac{1}{n+q-1}\left(\sum_{j=1}^{N}\frac{1}{\varphi(z_{j})}z_{j}\alpha_{j}\right)F_{q}([z],v_{i})=\frac{1}{\varphi(z_{i})}\alpha_{i}; \end{align*} $$
that is
$$ \begin{align*}c\varphi(z_{i})F_{q}([z],v_{i})=\alpha_{i},\end{align*} $$
where
$$ \begin{align*}c=\frac{1}{n+q-1}\sum_{j=1}^{N}\frac{1}{\varphi(z_{j})}z_{j}\alpha_{j}\end{align*} $$
is a constant that only depends on
$z_{j}. $
Let
$P=[z]$
. Then, the existence of P is proven.
We now show (3.5). Assume that it fails for some
$i_{0}$
. Let
$\tilde {z} \in \mathbb {R}_{+}^{N}$
be such that
$\tilde {z}=h_{[z]}(v_{i})$
. By
$h_{[f]}\le f$
, we have
$\tilde {z_{i_{0}}}<z_{i_{0}}$
and
$\tilde {z_{i}}\le z_{i}$
for
$i\ne i_{0}$
. Note that
$[z]=[\tilde {z}]$
, and consequently,
$I_{q}([\tilde {z}])=\left | \mu \right | $
. By definition of
$\Phi _{\phi }$
and
$\xi _{\phi },$
we have
$$ \begin{align*}\Phi_{\phi}(\tilde{z},\xi_{\phi}(\tilde{z})) <\Phi_{\phi}(z,\xi_{\phi}(\tilde{z})) \le \Phi_{\phi}(z,\xi_{\phi}(z)) =\Phi_{\phi}(z,o).\end{align*} $$
This is a contradiction to z being a minimizer.
Theorem 3.6 Let
$q>0$
, and
$\mu $
be as given in (3.1). Suppose
$\varphi :(0,\infty )\to (0,\infty )$
is differentiable and strictly increasing, and
$\varphi (s)$
tends to
$0$
as
$s\to 0^{+}$
such that
$\phi (t)=\int _{0}^{t}\frac {1}{\varphi (s)}\mathrm {d}s$
exists for every positive t. Then, there exists a polytope
$P\in \mathcal {P}(v_{1},\dots ,v_{N})$
containing the origin in its interior such that
$$ \begin{align*}c\varphi(h_{P})\mathrm{d}F_{q}(P,\cdot)=\mathrm{d}\mu.\end{align*} $$
Proof We consider the minimization problem (3.4). Let
$z^{l}\in \mathbb {R}^{N}$
be a minimizing sequence; that is,
$I_{q}([z^{l}])=\left | \mu \right | $
and
$$ \begin{align*}\lim_{l\to\infty}\Phi_{\phi}(z^{l},\xi_{\phi}(z^{l}))=\inf \left \{ \Phi_{\phi}(z,\xi_{\phi}(z)): z\in \mathbb{R}^{N}, I_{q}([z])=\left | \mu \right | \right \}.\end{align*} $$
Note that by translation invariance of
$I_{q}$
and the simple fact that
$$ \begin{align*}\Phi_{\phi}(z,\xi)=\Phi_{\phi}(z^{\prime},o),\end{align*} $$
where
$z_{j}^{\prime}=z_{j}-\xi \cdot v_{j},$
we can assume without loss of generality that
$\xi _{\phi }(z^{l})=o.$
Moreover, by the definition of
$\Phi _{\phi }$
, it must be the case that
$$ \begin{align*}z_{j}^{l}=h_{[z^{l}]}(v_{j})\end{align*} $$
by Lemma 3.5. The fact that
$o=\xi _{\phi }(z^{l})\in \mathrm{int}[z^{l}]$
now implies that
$z_{j}^{l}>0.$
Set
$\zeta (r)=(r,\dots ,r)\in \mathbb {R}^{N}.$
Then, by the homogeneity of
$I_{q}$
, we may find
$r_{0}>0$
such that
$$ \begin{align*}I_{q}([\zeta(r_{0})])=\left | \mu \right | .\end{align*} $$
Therefore,
$$ \begin{align} \lim_{l\to\infty}\Phi_{\phi}(z^{l},o)\le&{} \Phi_{\phi}(\zeta(r_{0}),\xi_{\phi}(\zeta(r_{0})))\notag\\ =&\sum_{j=1}^{N}\phi(r_{0}-\xi_{\phi}(\zeta(r_{0}))\cdot v_{j})\alpha_{j}\notag\\ \le&\sum_{j=1}^{N}\phi(2r_{0})\alpha_{j} <\infty, \end{align} $$
where by Lemma 3.2, we used the fact that
$\xi _{\phi }(\zeta (r_{0}))\in \mathrm{int}[\zeta (r_{0})].$
However, if we set
$L_{l}=\max _{j}z_{j}^{l},$
then
$$ \begin{align} \Phi_{\phi}(z^{l},o)=\sum_{j=1}^{N}\phi(z_{j}^{l})\alpha_{j}\ge \phi(L_{l})\min_{j}\alpha_{j}. \end{align} $$
By (3.7) and (3.8),
$z^{l}$
is uniformly bounded. Therefore, we may assume that
$z^{l}\to z^{0}$
for some
$z^{0}\in \mathbb {R}^{N}$
. By continuity of
$I_{q}$
, we have
$I_{q}([z^{0}])=\left | \mu \right | ,$
which implies that
$[z^{0}]$
contains a nonempty interior. Lemma 3.3 now implies that
$$ \begin{align*}\xi_{\phi}(z^{0})=\lim_{l\to\infty}\xi_{\phi}(z^{l})=o.\end{align*} $$
This and the fact that
$\xi _{\phi }(z^{0})\in \mathrm{int}[z^{0}]$
imply that
$z^{0}\in \mathbb {R}_{+}^{N}$
. Moreover, by the definition of
$\Phi _{\phi }$
, we have
$$ \begin{align*}\Phi_{\phi}(z^{0},o)=\lim_{l\to \infty}\Phi_{\phi}(z^{l},o)=\inf \left \{ \Phi_{\phi}(z,\xi_{\phi}(z)): z\in \mathbb{R}^{N}, I_{q}([z])=\left | \mu \right | \right \}.\end{align*} $$
Lemma 3.5 now implies the existence of P.
Funding
This study was funded by National Nature Science Foundation of China Grant No.12071334 and No.12071277.
Competing interest
The authors have no competing interest to declare.
