Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2025-01-05T15:31:29.843Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct Product Decompositions of Elation Groups

Published online by Cambridge University Press:  20 November 2018

Julia M. Nowlin Brown
Julia M. Nowlin Brown*
Affiliation:
Department of Mathematics, York University, 4700 Keele Street, Downsview, Ontario, Canada. M3J 1P3
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a collineation group of a projective plane π. Let E be the subgroup generated by all elations in G. In the case that π is finite and G fixes no point or line, F. Piper [6; 7] has proved that if G contains certain combinations of perspectivities, then E is isomorphic to 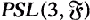for some finite field g.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 20 , Issue 2 , 01 June 1977 , pp. 173 - 182
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Albert, A. A. and Sandler, R., An introduction to finite projective planes, (Holt, Rinehart and Winston. New York, 1968).Google Scholar
2. André, J., Über Perspektivitäten in endlichen projektiven Ebenen, Arch. Math. 6 (1955), 29-32.Google Scholar
3. Coxeter, H. S. M., Projective Geometry, 2nd ed. (University of Toronto Press, Toronto, 1974).Google Scholar
4. Hering, C., Eine Charakterisierung der endlichen zweidimensionalen projektiven Gruppen, Math. Z. 82 (1963), 152-175.Google Scholar
5. Hering, C., On shears of translation planes, Abh. Math. Sem. Univ. Hamburg 37 (1972), 258-268.Google Scholar
6. Piper, F., Collineation groups containing dations. I, Math. Z. 89 (1965), 181-191.Google Scholar
7. Piper, F., Collineation groups containing homologies, J. Algebra 6 (1967), 256-269.Google Scholar