Hostname: page-component-5cf477f64f-fcbfl Total loading time: 0 Render date: 2025-04-08T07:48:44.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Dirac Delta Functions Via Nonstandard Analysis

Published online by Cambridge University Press:  20 November 2018

A. H. Lightstone  and
Kam Wong
A. H. Lightstone
Affiliation:
Queen's University
Kam Wong
Affiliation:
Queen's University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

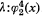We recall that a Dirac delta function δ(x) in the real number system is the idealization of a function that vanishes outside a "short" interval and satisfies 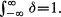It is conceived as a function δ for which δ(0)=+ ∞, δ(t)=0 if t≠0, and 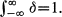This function should possess the "sifting property" 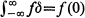for any continuous function f. Even though certain sequences of functions are used, via a limit operation, to approximate a Dirac delta function (for details, see [3] and [4]), no function in 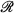has these properties.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 5 , 01 December 1975 , pp. 759 - 762
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Robinson, A., Non-standard Analysis, North-Holland Amsterdam 1966.Google Scholar
2. Kelemen, P.J. and Robinson, A., The Non-standard : Model 1. The Technique of Nonstandard Analysis in Theoretical Physics, J. Math. Phys., Vol. 13, No. 12, Dec. 1972.Google Scholar
3. Erdélyi, A., Operation Calculus and GeneralizedFunctions, Holt, Rinehart and Winston, Inc., 1962.Google Scholar
4. Pol, Balth. van der and Bremmer, H., Operational Calculus; Cambridge University Press, 1955.Google Scholar