Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T14:04:43.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimension Functions of Self-Affine Scaling Sets

Published online by Cambridge University Press:  20 November 2018

Xiaoye Fu  and
Jean-Pierre Gabardo
Xiaoye Fu
Affiliation:
Department of Mathematics, the Chinese University of Hong Kong, Hong Kong e-mail: [email protected]
Jean-Pierre Gabardo
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, ON, L8S 4K1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, the dimension function of a self-affine generalized scaling set associated with an 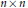$n\,\times \,n$ integral expansive dilation 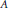$A$ is studied. More specifically, we consider the dimension function of an 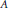$A$-dilation generalized scaling set 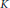$K$ assuming that 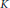$K$ is a self-affine tile satisfying 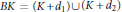$BK\,=\,\left( K\,+\,{{d}_{1}} \right)\,\cup \,\left( K\,+\,{{d}_{2}} \right)$, where 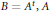$B\,=\,{{A}^{t}},\,A$ is an 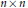$n\,\times \,n$ integral expansive matrix with 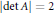$\left| \det \,A \right|\,=\,2$, and 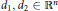${{d}_{1}},\,{{d}_{2}}\,\in \,{{\mathbb{R}}^{n}}$. We show that the dimension function of 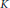$K$ must be constant if either 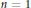$n\,=1$ or 2 or one of the digits is 0, and that it is bounded by 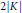$2\left| K \right|$ for any $n$.

Keywords

42C40scaling setself-affine tileorthonormal multiwaveletdimension function
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 4 , 01 December 2013 , pp. 745 - 758
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Auscher, P., Solution of two problems on wavelets. J. Geom. Anal. 5 (1995), 181–236. http://dx.doi.org/10.1007/BF02921675 Google Scholar
[2] Baggett, L., Carey, A., Moran, W., and Ohring, P., General existence theorems for orthonormal wavelets, an abstract approach. Publ. Res. Inst. Math. Sci. 31 (1995), 95–111. http://dx.doi.org/10.2977/prims/1195164793 Google Scholar
[3] Baggett, L.W., An abstract interpretation of the wavelet dimension function using group representations. J. Funct. Anal. 173 (2000), 1–20. http://dx.doi.org/10.1006/jfan.1999.3551 Google Scholar
[4] Baggett, L.W., Medina, H. A., and Merrill, K. D., Generalized multi-resolution analyses and a construction procedure for all wavelet sets in Rn. J. Fourier Anal. Appl. 5 (1999), 563–573. http://dx.doi.org/10.1007/BF01257191 Google Scholar
[5] Bownik, M. and Speegle, D., The wavelet dimension function for real dilations and dilations admitting non-MSF wavelets. In: Approximation Theory X:Wavelet splines, and applications, Vanderbilt University Press, Nashville, 2002, 63–85.Google Scholar
[6] Bownik, M. and Hoover, K., Dimension functions of rationally dilated GMRAs and wavelets. J. Fourier Anal. Appl. 15 (2009), 585–615. http://dx.doi.org/10.1007/s00041-009-9058-0 Google Scholar
[7] Bownik, M., Rzeszotnik, Z., and Speegle, D., A characterization of dimension functions of wavelets. Appl. Comput. Harmon. Anal. 10 (2001), 71–92. http://dx.doi.org/10.1006/acha.2000.0327 Google Scholar
[8] Dai, X., Larson, D., and Speegle, D., Wavelet sets in RN.J. Fourier Anal. Appl. 3 (1997), 451–456. http://dx.doi.org/10.1007/BF02649106 Google Scholar
[9] Daubechies, I., Ten lectures on wavelets. CBMS-NSF Regional Conf. Ser. in Appl. Math. 61, Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 1992.Google Scholar
[10] Daubechies, I. and Lagarias, J. C., Two-scale difference equations I: existence and global regularity of solutions. SIAM J. Math. Anal. 22 (1991), 1388–1410. http://dx.doi.org/10.1137/0522089 Google Scholar
[11] Fang, X. and Wang, X., Construction of minimally-supported-frequencies wavelets. J. Fourier Anal. Appl. 2 (1996), 315–327.Google Scholar
[12] Frazier, M., Garrigos, G., Wang, K., and Weiss, G., A characterization of functions that generate wavelet and related expansion. J. Fourier Anal. Appl. 3 (1997), 883–906. http://dx.doi.org/10.1007/BF02656493 Google Scholar
[13] Gripenberg, G., A necessary and sufficient condition for the existence of a father wavelet. Stud. Math. 114 (1995), 207–226.Google Scholar
[14] Gröchenig, K. and Haas, A., Self-similar lattice tilings. J. Fourier Anal. Appl. 1 (1994), 131–170. http://dx.doi.org/10.1007/s00041-001-4007-6 Google Scholar
[15] Gu, Q. and Han, D., On multiresolution analysis (MRA) wavelets in RN.J. Fourier Anal. Appl. 6 (2000), 437–447. http://dx.doi.org/10.1007/BF02510148 Google Scholar
[16] Gröchenig, K. and Madych, W., Multiresolution analysis. haar bases, and self-similar tilings of Rn. IEEE Trans. Inform. Theory 38 (1992), 556–568. http://dx.doi.org/10.1109/18.119723 Google Scholar
[17] Gabardo, J.-P. and Yu, X., Construction of wavelet sets with certain self-similarity properties. J. Geom. Anal. 14 (2004), 629–651. http://dx.doi.org/10.1007/BF02922173 Google Scholar
[18] Hernández, E., Wang, X., and Weiss, G., Smoothing minimally supported frequency (MSF) wavelets: Part I. J. Fourier Anal. Appl. 3 (1997), 329–340.Google Scholar
[19] Hernández, E. and Weiss, G., A first course on wavelets. Stud. in Adv. Math., CRC Press, Boca Raton, FL, 1996.Google Scholar
[20] Lagarias, J. C. and Wang, Y., Haar-type orthonormal wavelet bases in R2. J. Fourier Anal. Appl. 2 (1995), 1–14. http://dx.doi.org/10.1007/s00041-001-4019-2 Google Scholar
[21] Lagarias, J. C. and Wang, Y., Integral self-affine tiles in Rn. I. Standard and nonstandard digit sets. J. London Math. Soc. 54 (1996), 161–179. http://dx.doi.org/10.1112/jlms/54.1.161 Google Scholar
[22] Lagarias, J. C. and Wang, Y., Self-affine tiles in Rn. Adv. Math. 121 (1996), 21–49. http://dx.doi.org/10.1006/aima.1996.0045 Google Scholar
[23] Lagarias, J. C. and Wang, Y., Integral self-affine tiles in Rn, Part II: Lattice tilings. J. Fourier Anal. Appl. 3 (1997), 83–102. http://dx.doi.org/10.1007/BF02647948 Google Scholar
[24] Lemarié-Rieusset, P.-G. Existence de “fonction-pére” pour les ondelettes `a support compact. C. R. Acad. Sci. Paris Sér. I Math. 314 (1992), 17–19.Google Scholar
[25] Lemarié-Rieusset, P.-G., Sur l’existence des analyses multi-résolutions en théorie des ondelettes. Rev. Mat. Iberoam. 8 (1992), 457–474. http://dx.doi.org/10.4171/RMI/131 Google Scholar
[26] Mallat, S. G., Multiresolution approximations and wavelet orthonormal bases of L2(R). Trans. Amer. Math. Soc. 315 (1989), 69–87.Google Scholar
[27] Ron, A. and Shen, Z., The wavelet dimension function is the trace function of a shift-invariant system. Proc. Amer. Math. Soc. 131 (2003), 1385–1398. http://dx.doi.org/10.1090/S0002-9939-02-06677-7 Google Scholar
[28] Strichartz, R. S., Wavelets and self-affine tilings. Constr. Approx. 9 (1993), 327–346. http://dx.doi.org/10.1007/BF01198010 Google Scholar
[29] Wang, X., The study of wavelets from the properties of their Fourier transform. Ph.D. thesis, Washington University in St. Louis, 1995.Google Scholar