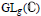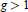Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Qingjie
and
Zhong, Weiting
2015.
Dihedral Groups of Order 2p of Automorphisms of Compact Riemann Surfaces of Genus p – 1.
Canadian Mathematical Bulletin,
Vol. 58,
Issue. 1,
p.
196.
Reyes-Carocca, Sebastián
2021.
On pq-fold regular covers of the projective line.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 115,
Issue. 1,