This packing problem is obviously equivalent to the problem of locating six points Pi(l ≤ i ≤ 6) in a- closed unit cube C such that 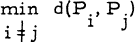is as large as possible, where d(Pi, Pj) denotes the distance between Pi and Pj. We shall prove that this minimum distance cannot exceed 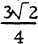(= m, say), and that 4 it attains this value only if the points form a configuration which is congruent to the one of the points Ri(l≤i≤6) shown in fig. 1. Note that 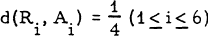, and so the six points are the vertices of a regular octahedron.