Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T16:17:51.505Z Has data issue: false hasContentIssue false
  • English
  • Français

A Decomposition Theorem for Positive Superharmonic Functions

Published online by Cambridge University Press:  20 November 2018

Sirkka-Liisa Eriksson-Bique
Sirkka-Liisa Eriksson-Bique*
Affiliation:
Department of Mathematics University of Joensuu SF-80101 Joensuu, Finland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a harmonic space in the sense of C. Constantinescu and A. Cornea. We show that, for any subset E of X, a positive superharmonic function u on X has a representation u = p + h, where p is the greatest specific minorant of u satisfying 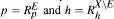. This result is a generalization of a theorem of M. Brelot. We also state some characterizations of extremal superharmonic functions.

Keywords

31D0506A10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 33 , Issue 3 , 01 September 1990 , pp. 286 - 296
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Arsove, M. G. and Leutwiler, H., Algebraic potential theory, Mem. Amer. Math. Soc. 23, No. 226 (1980).Google Scholar
2. Bliedtner, J. and Hansen, W., Potential theory (Springer-Verlag, Berlin-Heidelberg-New York, 1986).Google Scholar
3. Boboc, N., Bucur, Gh. and Cornea, A., Order and convexity in potential theory: H-cones (Lecture Notes in Mathematics 853, Springer-Verlag, Berlin-Heidelberg-New York, 1981).Google Scholar
4. Brelot, M., On topologies and boundaries in potential theory (Lecture Notes in Mathematics 175, Springer-Verlag, Berlin-Heidelberg-New York, 1971).Google Scholar
5. Brelot, M., Sur le théorème de partition de Mme R.-M. Hervé, Rocky Mountain J. of Math. 10 (1) (1980), 293–302.Google Scholar
6. Constantinescu, C. and Cornea, A., Potential theory on harmonie spaces (Springer-Verlag, Berlin- Heidelberg-New York, 1972).Google Scholar
7. Gowrisankaran, K., Extreme harmonie functions and boundary value problems, Ann. Inst. Fourier 13 (2) (1963), 307–356.Google Scholar
8. Gowrisankaran, K., Extreme harmonic functions and boundary value problems II, Math. Z. 94 (1966), 256–270.Google Scholar
9. Gowrisankaran, K., Fatou-Naim-Doob limit theorems in the axiomatic system of Brelot, Ann. Inst. Fourier 16 (2) (1966), 455–467.Google Scholar
10. R.-H. Hervé, Recherches axiomatiques sur la théorie des fonctions surharmoniques et du potentiel, Ann. Inst. Fourier 12 (1962), 415–571.Google Scholar
11. Nairn, L., Sur le role de la frontière de R.S. Martin dans la théorie du potentiel, Ann. Inst. Fourier 7 (1957), 183–285.Google Scholar
12. Riesz, F., Über die subharmonischen Funktionen und ihre Rolle in der Funktionentheorie und in der Potentialtheorie, Acta Sci. Math. (Szeged) 2 (2) (1925), 87–100.Google Scholar
13. Sieveking, M., Integraldarstellung superharmonischer Funktionen mit Anwendung auf parabolische Differentialgleichungen, In Seminair über F'otentialtheorie, Lecture Notes in Mathematics 69, Springer-Verlag, Berlin-Heidelberg-New York, 1971, 13–68.Google Scholar