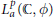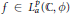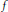Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Huang, Hansong
and
Izuchi, Kou Hei
2024.
Cyclic vectors in Fock-type spaces in multi-variable case.
Annals of Functional Analysis,
Vol. 15,
Issue. 2,