Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T10:55:18.652Z Has data issue: false hasContentIssue false
  • English
  • Français

Cyclic Surgery Between Toroidal Surgeries

Published online by Cambridge University Press:  20 November 2018

Masakazu Teragaito
Masakazu Teragaito*
Affiliation:
Department of Mathematics and Mathematics Education, Hiroshima University, Higashi-hiroshima, Japan 739-8524 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that there is an infinite family of hyperbolic knots such that each knot admits a cyclic surgery 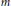$m$ whose adjacent surgeries 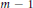$m\,-\,1$ and 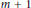$m\,+\,1$ are toroidal. This gives an affirmative answer to a question asked by Boyer and Zhang.

Keywords

57M25cyclic surgerytoroidal surgery
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 3 , 01 September 2011 , pp. 556 - 560
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Bleiler, S. A. and Litherland, R. A., Lens spaces and Dehn surgery. Proc. Amer. Math. Soc. 107(1989), no. 4, 1127–1131.Google Scholar
[2] Boyer, S. and Zhang, X., Cyclic surgery and boundary slopes. In: Geometric topology (Athens, GA, 1993), AMS/IP Stud. Adv. Math., 2.1, American Mathematical Society, Providence, RI, 1997, pp. 62–79.Google Scholar
[3] Culler, M., Gordon, C. McA., Luecke, J., and Shalen, P., Dehn surgery on knots. Ann. of Math. 125(1987), no. 2, 237–300. doi:10.2307/1971311Google Scholar
[4] Eudave-Muñoz, M., Non-hyperbolic manifolds obtained by Dehn surgery on hyperbolic knots. In: Geometric topology (Athens, GA, 1993), AMS/IP Stud. Adv. Math., 2.1, American Mathematical Society, Providence, RI, 1997, 35–61.Google Scholar
[5] Eudave-Muñoz, M. and Wu, Y.-Q., Nonhyperbolic Dehn fillings on hyperbolic 3-manifolds. Pacific J. Math. 190(1999), no. 2, 261–275. doi:10.2140/pjm.1999.190.261Google Scholar
[6] Gordon, C. McA. and Luecke, J., Knots are determined by their complements. J. Amer. Math. Soc. 2(1989), no. 2, 371–415.Google Scholar
[7] Morgan, J. and Tian, G., Ricci flow and the Poincaré conjecture. Clay Mathematics Monographs, 3, American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA, 2007.Google Scholar
[8] Moser, L., Elementary surgery along a torus knot. Pacific J. Math. 38(1971), 737–745.Google Scholar
[9] Stallings, J. R., Constructions of fibred knots and links. In: Algebraic and geometric topology (Proc. Sympos. Pure Math., Stanford Univ., Stanford, Calif., 1976), Part 2, Proc. Sympos. Pure Math., XXXII, American Mathematical Society, Providence, RI, 1978, pp. 55–60.Google Scholar
[10] Wang, S. C., Cyclic surgery on knots. Proc. Amer. Math. Soc. 107(1989), no. 4, 1091–1094.Google Scholar
[11] Wu, Y. Q., Cyclic surgery and satellite knots. Topology Appl. 36(1990), no. 3, 205–208. doi:10.1016/0166-8641(90)90045-4Google Scholar
[12] Zhang, X., Cyclic surgery on satellite knots. Glasgow Math. J. 33(1991), no. 2, 125–128. doi:10.1017/S0017089500008144Google Scholar