Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-30T22:48:22.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Cup Products in Sheaf Cohomology

Published online by Cambridge University Press:  20 November 2018

J. F. Jardine
J. F. Jardine*
Affiliation:
Mathematics Department, University of Western Ontario
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be an algebraically closed field, and let l be a prime number not equal to char(k). Let X be a locally fibrant simplicial sheaf on the big étale site for k, and let Y be a k scheme which is cohomologically proper. Then there is a Künneth-type isomorphism

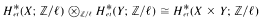
which is induced by an external cup-product pairing. Reductive algebraic groups G over k are cohomologically proper, by a result of Friedlander and Parshall. The resulting Hopf algebra structure on 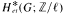may be used together with the Lang isomorphism to give a new proof of the theorem of Friedlander-Mislin which avoids characteristic 0 theory. A vanishing criterion is established for the Friedlander-Quillen conjecture.

Keywords

14F2018F25
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 29 , Issue 4 , 01 December 1986 , pp. 469 - 477
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Brown, K. S., Abstract homotopy theory and generalized sheaf cohomology, Trans. AMS 186 (1973), pp. 419–458.Google Scholar
2. Friedlander, E. M., Étale Homotopy of Simplicial Schemes, Princeton University Press, Princeton (1982).Google Scholar
3. Friedlander, E. M. and Mislin, G., Cohomology of classifying spaces of complex Lie groups and related discrete groups, Comment. Math. Helv. 59 (1984), pp. 347–361.Google Scholar
4. Friedlander, E. M. and Parshall, B., Étale cohomology of reductive groups, Springer Lecture Notes in Math. 854 (1981), pp. 127–140.Google Scholar
5. Jardine, J. F., Simplicial objects in a Grothendieck topos, Preprint.Google Scholar
6. Milne, J. S., Étale Cohomology, Princeton University Press, Princeton (1980).Google Scholar
7. Steinberg, R., Endomorphisms of linear algebraic groups, Memoirs of the AMS 80 (1980).Google Scholar