Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-16T15:49:19.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Criteria for periodicity and an application to elliptic functions

Part of: Difference equations Differential and difference algebra Curves Difference and functional equations

Published online by Cambridge University Press:  14 August 2020

Ehud de Shalit
Ehud de Shalit*
Affiliation:
Einstein Institute of Mathematics, Hebrew University of Jerusalem, Jerusalem, Israel
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let P and Q be relatively prime integers greater than 1, and let f be a real valued discretely supported function on a finite dimensional real vector space V. We prove that if 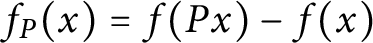$f_{P}(x)=f(Px)-f(x)$ and 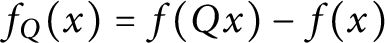$f_{Q}(x)=f(Qx)-f(x)$ are both 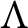$\Lambda $ -periodic for some lattice 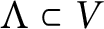$\Lambda \subset V$ , then so is f (up to a modification at 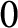$0$ ). This result is used to prove a theorem on the arithmetic of elliptic function fields. In the last section, we discuss the higher rank analogue of this theorem and explain why it fails in rank 2. A full discussion of the higher rank case will appear in a forthcoming work.

Keywords

Difference equationsperiodic functionselliptic functions

MSC classification

Primary: 39A10: Difference equations, additive 12H10: Difference algebra
Secondary: 14H52: Elliptic curves
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 3 , September 2021 , pp. 530 - 540
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was supported by ISF grant 276/17.

References

Adamczewski, B., Mahler’s method. Documenta Math. Extra Vol. Mahler Selecta (2019), 95–122.Google Scholar
Adamczewski, B. and Bell, J. P., A problem about Mahler functions . Ann. Sci. Norm. Super. Pisa 17(2017), 1301–1355.Google Scholar
Cobham, A., On the Hartmanis-Stearns problem for a class of tag machines. In: Conference Record of 1968 Ninth Annual Symposium on Switching and Automata Theory, Schenectady, NY, 1968, pp. 51–60.Google Scholar
de Shalit, E., Elliptic $(p,q)$ -difference modules. Preprint, 2020. arXiv:2007.09508.Google Scholar
de Shalit, E., Notes on the conjecture of Loxton and van der Poorten. Seminar notes. http://www.ma.huji.ac.il/˜deshalit/new_site/ln.htm Google Scholar
Schäfke, R. and Singer, M. F., Consistent systems of linear differential and difference equations . J. Eur. Math. Soc. 21(2019), 2751–2792. https://doi.org/10.4171/JEMS/891 CrossRefGoogle Scholar
van der Poorten, A. J., Remarks on automata, functional equations and transcendence . In: Séminaire de Théorie des Nombres de Bordeaux (1986–1987), Exp. No. 27, 11 pp.Google Scholar
van der Put, M. and Singer, M. F., Galois theory of difference equations. Lecture Notes in Mathematics, 1666, Springer-Verlag, Berlin, 1997. https://doi.org/10.1007/BFb0096118 CrossRefGoogle Scholar