Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-07-01T12:25:30.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Cover Product and Betti Polynomial of Graphs

Published online by Cambridge University Press:  20 November 2018

Aurora Llamas  and
Josá Martínez–Bernal
Aurora Llamas
Affiliation:
Departamento de Matem´aticas, Cinvestav-IPN, A.P. 14-740, 07000 Máxico D.F.. e-mail: [email protected], e-mail: [email protected]
Josá Martínez–Bernal
Affiliation:
Departamento de Matem´aticas, Cinvestav-IPN, A.P. 14-740, 07000 Máxico D.F.. e-mail: [email protected], e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The cover product of disjoint graphs 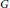$G$ and $H$ with fixed vertex covers 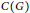$C\left( G \right)$ and 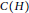$C\left( H \right)$, is the graph $G\circledast H$ with vertex set $V\left( G \right)\cup V\left( H \right)$ and edge set

$$E\left( G \right)\,\cup \,E\left( H \right)\,\cup \,\left\{ \left\{ i,\,j \right\}\,:\,i\,\in \,C\left( G \right),\,j\,\in \,C\left( H \right) \right\}.$$

We describe the graded Betti numbers of $G\circledast H$ in terms of those of 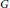$G$ and $H$. As applications we obtain: (i) For any positive integer k there exists a connected bipartite graph 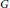$G$ such that 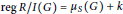$\text{reg}\,R/I\left( G \right)\,=\,{{\mu }_{s}}\left( G \right)\,+\,k$, where, 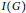$I\left( G \right)$ denotes the edge ideal of 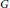$G$, $\text{reg}\,\text{R/I}\left( G \right)$ is the Castelnuovo–Mumford regularity of $\text{R/I}\left( G \right)$ and 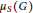${{\mu }_{s}}\left( G \right)$ is the induced or strong matching number of 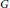$G$; (ii)The graded Betti numbers of the complement of a tree depends only upon its number of vertices; (iii)The $h$-vector of 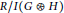$R/I\left( G\circledast H \right)$ is described in terms of the 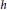$h$-vectors of $\text{R/I}\left( G \right)$ and 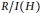$R/I\left( H \right)$. Furthermore, in a different direction, we give a recursive formula for the graded Betti numbers of chordal bipartite graphs.

Keywords

13D0205E45Castelnuovo–Mumford regularitychordal bipartite graphedge idealgraded Betti numberinduced matching numbermonomial ideal
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 320 - 333
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Abbott, J., Bigatti, A. M., and G. Lagoio, CoCoA-5: A system for doing computations in commutative algebra, http://cocoa.dima.unige.itGoogle Scholar
[2] Bondy, A. and Murty, U.S.R., Graph theory. Graduate Texts in Mathematics, 244, Springer, New York, 2008.Google Scholar
[3] Bruns, W. and Herzog, J., Cohen-Macaulay rings. Cambridge Studies in Advanced Mathematics, 39, Cambridge University Press, Cambridge, 1993.Google Scholar
[4] Corso, A. and Nagel, U., Monomial and toric ideals associated to Ferrers graphs. Trans. Amer. Math. Soc. 361 (2009), no. 3, 1371–1395. http://dx.doi.org/10.1090/S0002-9947-08-04636-9 Google Scholar
[5] de Alwis, T., Free minimal resolutions. Comm. Algebra 21 (1993), no. 12, 4575–4585. http://dx.doi.org/10.1080/00927879308824817 Google Scholar
[6] de Alwis, T., Free minimal resolutions and the Betti numbers of the suspension of an n-agon. Int. J. Math. Math. Sci. 23 (2000), no. 3, 211–216. http://dx.doi.Org/10.1155/SO161171200001563 Google Scholar
[7] Dirac, G. A., On rigid circuit graphs. Abh. Math. Sem. Univ. Hamburg 25 (1961), 71–76. http://dx.doi.org/10.1007/BF02992776 Google Scholar
[8] Dochtermann, A. and Engstrôm, A., Algebraic properties of edge ideals via combinatorial topology. Electron. J. Combin. 16 (2009), no. 2, Research Paper 2.Google Scholar
[9] Ferrarello, D. and Frôberg, R., The Hilbert series of the clique complex. Graphs Combin. 21 (2005), no. 4, 401–405. http://dx.doi.Org/10.1007/s00373-005-0634-z Google Scholar
[10] Francisco, C. A. and A. Van Tuyl, Sequentially Cohen-Macaulay edge ideals. Proc. Amer. Math. Soc. 135 (2007), no. 8, 2327–2337. http://dx.doi.org/10.1090/S0002-9939-07-08841-7 Google Scholar
[11] Golumbic, M. Ch. and Lewenstein, M., New results on induced matchings. Discrete Appl. Math. 101 (2000), no. 1, 157–165. http://dx.doi.org/10.1016/S0166-218X(99)00194-8 Google Scholar
[12] Fulkerson, D. R. and Gross, O. A., Incidence matrices and interval graphs. Pacific J. Math. 15 (1965), 835–855. http://dx.doi.org/10.2140/pjm.1965.15.835 Google Scholar
[13] Hà, H. T and Van Tuyl, A., Splittable ideals and the resolution of monomial ideals. J. Algebra 309 (2007), no. 1, 405–425. http://dx.doi.Org/10.1016/j.jalgebra.2OO6.O8.O22 Google Scholar
[14] Hà, H. T and Van Tuyl, A., Resolutions of square-free monomial ideals via facet ideals: a survey. In: Algebra, geometry and their interactions, Contemp. Math., 448, American Mathematical Society, Providence, RI, 2007, pp. 91–117.Google Scholar
[15] Hayward, R., Hoàng, C., and Maffray, F., Optimizing weakly triangulated graphs. Graphs Combin. 5 (1989), no. 4, 339–349. http://dx.doi.Org/10.1007/BF01788689 Google Scholar
[16] Hochster, M., Cohen-Macaulay rings, combinatorics, and simplicial complexes. In: Ring theory, II, (Proc. Second Cond., Univ. Oklahoma, Norman, Okla., 1975), Lecture Notes in Pure and Appl. Math., 26, Dekker, New York, 1977, pp. 171–223.Google Scholar
[17] Jacques, S., Betti numbers of graph ideals. Ph.D. Thesis, University of Sheffield, 2004. arxiv:math/0410107Google Scholar
[18] Jacques, S. and Katzman, M., The Betti numbers of forests. arxiv:math/0501226v2Google Scholar
[19] Katzman, M., Characteristic-Independence of Betti numbers of graph ideals. J. Combin. Theory Ser. A 113 (2006), no. 3, 435–454. http://dx.doi.Org/10.1016/j.jcta.2OO5.04.005 Google Scholar
[20] Kummini, M., Regularity, depth and arithmetical rank of bipartite edge ideals. J. Algebraic Combin. 30 (2009), no. 4, 429–445. http://dx.doi.org/10.1007/s10801–009-0171-6 Google Scholar
[21] Martinez-Bernal, J., Renteria, C., and Villarreal, R.H., Combinatorics of symbolic Rees algebras of edge ideals of clutters. Contemp. Math. 555 (2011), 151–164.Google Scholar
[22] Miller, E. and Sturmfels, B., Combinatorial commutative algebra. Graduate Texts in Mathematics, 227, Springer-Verlag, New York, 2005.Google Scholar
[23] Morey, S. and Villarreal, R. H., Edge ideals: Algebraic and combinatorial properties. In: Progress in commutative algebra 1, de Gruyter, Berlin, 85–126.Google Scholar
[24] Mousivand, A., Algebraic properties of product of graphs. Comm. Algebra 40 (2012), no. 11, 4177–4194. http://dx.doi.org/10.1080/0092 7872.2011.605408 Google Scholar
[25] Peeva, I. and Stillman, M., Open problems on syzygies and Hilbert functions. J. Commut. Algebra 1 (2009), no. 1, 159–195. http://dx.doi.org/10.1216/JCA-2009–1-1-159 Google Scholar
[26] Renteln, P., The Hilbert series of the face ring of a flag complex. Graphs Combin. 18 (2002), no. 3, 605–619. http://dx.doi.org/10.1007/s003730200045 Google Scholar
[27] Schrijver, A., Combinatorial optimization. Algorithms and Combinatorics, 24, Springer-Verlag, Berlin, 2003.Google Scholar
[28] Spinrad, J. P. and Sritharan, R., Algorithms for weakly triangulated graphs. Discrete Appl. Math. 59 (1995), no. 2, 181–191. http://dx.doi.Org/10.1016/0166–218X(93)E0161-Q Google Scholar
[29] Terai, N., Alexander duality theorem and Stanley-Reisner rings. Free resolutions of coordinate rings of projective varieties and related topics (Japanese) (Kyoto, 1998). Surikaisekikenkyusho Kokyuroku 1078 (1999), 174–184.Google Scholar
[30] Van Tuyl, A., Sequentially Cohen-Macaulay bipartite graphs: vertex decomposability and regularity. Arch. Math. 93 (2009), 451–459. http://dx.doi.Org/10.1007/s00013-009-0049-9 Google Scholar
[31] Villarreal, R. H., Cohen-Macaulay graphs. Manuscripta Math. 66 (1990), 277–293. http://dx.doi.org/10.1007/BF02568497 Google Scholar
[32] Whieldon, G., Jump sequences of edge ideals, arXiv : 1012.0108vl, 2010.Google Scholar
[33] Woodroofe, R., Vertex decomposable graphs and obstructions to shellability. Proc. Amer. Math. Soc. 137 (2009), no. 10, 3235–3246. http://dx.doi.org/10.1090/S0002-9939-09-09981-X Google Scholar
[34] Woodroofe, R., Matchings, coverings, and Castelnuovo-Mumford regularity. J. Commut. Algebra 6 (2014), no. 2, 287–304. http://dx.doi.org/10.1216/JCA-2014-6-2-287 Google Scholar