For a commutative ring 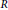$R$, a polynomial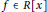$f\,\in \,R[x]$ is called separable if 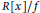$R[x]/f$ is a separable 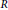$R$-algebra. We derive formulae for the number of separable polynomials when 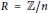$R\,=\,\mathbb{Z}/n$, extending a result of L. Carlitz. For instance, we show that the number of polynomials in 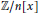$\mathbb{Z}/n[x]$ that are separable is 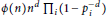$\phi (n){{n}^{d}}{{\prod }_{i}}(1\,-\,p_{i}^{-d})$, where 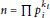$n\,=\,\prod p_{i}^{{{k}_{i}}}$ is the prime factorisation of $n$ and 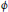$\phi $ is Euler’s totient function.