Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T07:16:21.342Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting Multiple Cyclic Choices Without Adjacencies

Published online by Cambridge University Press:  20 November 2018

Alice McLeod  and
William Moser
Alice McLeod
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, Quebec, H3A2K6
William Moser
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, Quebec, H3A2K6
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a particularly elementary solution to the following well-known problem. What is the number of $k$-subsets 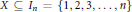$X\subseteq {{I}_{n}}=\left\{ 1,2,3,\ldots ,n \right\}$ satisfying “no two elements of 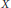$X$ are adjacent in the circular display of 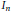${{I}_{n}}$”? Then we investigate a new generalization (multiple cyclic choices without adjacencies) and apply it to enumerating a class of 3-line latin rectangles.

Keywords

05A1905A05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 2 , 01 June 2005 , pp. 244 - 250
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Hall, M. Jr. Combinatorial Theory. Second edition. John Wiley, New York, 1986.Google Scholar
[2] Kaplansky, I., On a generalization of the “Problème des recontres”. Amer. Math. Monthly 46(1939), 159–161 Google Scholar
[3] Moser, W. and Pollack, R., A new identity and some applications. Canad. Math. Bull. 23(1980), 281–290.Google Scholar
[4] Riordan, J., Three-line Latin rectangles. Amer. Math. Monthly 51(1944), 450–452.Google Scholar
[5] Riordan, J., An Introduction to Combinarorial Analysis. John Wiley, New York, 1958.Google Scholar
[6] Touchard, J., Sur un problème de permutations. C. R. Acad. Sci. Paris 198(1934), 631–633.Google Scholar