Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-07-01T12:44:53.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Countable Dense Homogeneity in Powers of Zero-dimensional Definable Spaces

Published online by Cambridge University Press:  20 November 2018

Andrea Medini
Andrea Medini*
Affiliation:
Kurt Gödel Research Center for Mathematical Logic, University of Vienna, WGähringer Straße 25, A-1090 Wien, Austria. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that for a coanalytic subspace 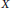$X$ of 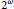${{2}^{\omega }}$, the countable dense homogeneity of 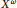${{X}^{\omega }}$ is equivalent to 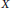$X$ being Polish. This strengthens a result of Hrušák and Zamora Avilés. Then, inspired by results of Hernández-Gutiérrez, Hrušák, and van Mill, using a technique of Medvedev, we construct a non-Polish subspace 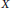$X$ of 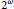${{2}^{\omega }}$ such that 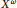${{X}^{\omega }}$ is countable dense homogeneous. This gives the first 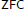$\text{ZFC}$ answer to a question of Hrušák and Zamora Avilés. Furthermore, since our example is consistently analytic, the equivalence result mentioned above is sharp. Our results also answer a question of Medini and Milovich. Finally, we show that if every countable subset of a zero-dimensional separable metrizable space 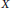$X$ is included in a Polish subspace of 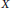$X$, then 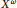${{X}^{\omega }}$ is countable dense homogeneous.

Keywords

54H0554G2054E52countable dense homogeneousinfinite powercoanalyticPolishλ'-set
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 334 - 349
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Anderson, R. D., Curtis, D. W., van Mill, J., A fake topological Hilbert space. Trans. Amer. Math. Soc. 272 (1982), no. 1, 311–321. http://dx.doi.org/10.1090/S0002-9947-1982-0656491-8 Google Scholar
[2] Arkhangel'skiï, A. V. and van Mill, J., Topological homogeneity. In: Recent Progress in General Topology III. Atlantis Press, 2014, pp. 1–68.Google Scholar
[3] Bartoszynski, T., Judah, H., and Ihoda, J., Set theory. On the structure of the real line. A K Peters, Ltd., Wellesley, MA, 1995.Google Scholar
[4] Dow, A. and Pearl, E., Homogeneity in powers of zero-dimensional first-countable spaces. Proc. Amer. Math. Soc. 125 (1997), no. 8, 2503–2510. http://dx.doi.org/10.1090/S0002-9939-97-03998-1 Google Scholar
[5] Engelking, R., General topology. Sigma Series in Pure Mathematics, 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[6] Fitzpatrick, B. Jr. and Zhou, H. X., Some open problems in densely homogeneous spaces. In: Open problems in topology, J. van Mill and G. M. Reed eds., North-Holland, Amsterdam, 1990, pp. 251–259.Google Scholar
[7] Fitzpatrick, B. Jr. and Zhou, H. X., Countable dense homogeneity and the Baire property. Topology Appl. 43 (1992), no. 1, 1–14. http://dx.doi.Org/10.1016/0166-8641(92)90148-S Google Scholar
[8] Halmos, P. R., Permutations of sequences and the Schroder-Bernstein theorem. Proc. Amer. Math. Soc. 19 (1968), 509–510.Google Scholar
[9] Hernandez-Gutierrez, R. and Hrusak, M., Non-meager P-filters are countable dense homogeneous. Colloq. Math. 130 (2013), no. 2, 281–289. http://dx.doi.org/10.4064/cm130-2-9 Google Scholar
[10] Hernândez-Gutiérrez, R., Hrusâk, M., and van Mill, J., Countable dense homogeneity and X-sets. Fund. Math. 226 (2014), no. 2, 157–172. http://dx.doi.Org/10.4064/fm226-2-5 Google Scholar
[11] Hrusak, M. and Zamora Avilés, B., Countable dense homogeneity of definable spaces. Proc. Amer. Math. Soc. 133 (2005), no. 11, 3429–3435. http://dx.doi.org/10.1090/S0002-9939-05-07858-5 Google Scholar
[12] Just, W., Mathias, A. R. D., K. Prikry, and P. Simon, On the existence of large p-ideals. J. Symbolic Logic 55 (1990), no. 2, 457–465. http://dx.doi.org/10.2307/2274639 Google Scholar
[13] Kechris, A. S., Classical descriptive set theory. Graduate Texts in Mathematics, 156, Springer-Verlag, New York, 1995.Google Scholar
[14] Knaster, B. and Reichbach, M., Notion d'homogénéité et prolongements des homéomorphies. Fund. Math. 40 (1953), 180–193.Google Scholar
[15] Kunen, K., Set theory. Studies in Logic (London), 34, College Publications, London, 2011.Google Scholar
[16] Kunen, K., Medini, A., and Zdomskyy, L., Seven characterizations of non-meager P-filters. arxiv:1311.1677Google Scholar
[17] Kuratowski, K., Topology. Vol. I. New éd., revised and augmented. Academic Press, New York-London; Panstwowe Wydawnictwo Naukowe, Warsaw, 1966.Google Scholar
[18] Lawrence, L. B., Homogeneity in powers of subspaces of the real line. Trans. Amer. Math. Soc. 350 (1998), no. 8, 3055–3064. http://dx.doi.org/10.1090/S0002-9947-98-02100-X Google Scholar
[19] Medini, A., Products and h-homogeneity. Topology Appl. 158 (2011), no. 18, 2520–2527. http://dx.doi.Org/10.1016/j.topol.2011.08.011 Google Scholar
[20] Medini, A., The topology of ultrafilters as subspaces of the Cantor set and other topics. Ph.D. Thesis. University of Wisconsin - Madison, ProQuest LLC, Ann Arbor, MI, 2013.Google Scholar
[21] Medini, A. and D. Milovich, The topology of ultrafilters as subspaces of2”. Topology Appl. 159 (2012), no. 5, 1318–1333. http://dx.doi.Org/10.1016/j.topol.2011.12.009 Google Scholar
[22] Medini, A. and L. Zdomskyy, Between Polish and completely Baire. Arch. Math. Logic 54 (2015), no. 1–2, 231–245. http://dx.doi.Org/10.1007/s00153-014-0409-4 Google Scholar
[23] Medvedev, S. V., On properties ofh-homogeneous spaces of first category. Topology Appl. 157 (2010), no. 18, 2819–2828. http://dx.doi.org/10.1016/j.topol.2010.08.021 Google Scholar
[24] Medvedev, S. V., On properties of h-homogeneous spaces with the Baire property. Topology Appl. 159 (2012), no. 3, 679–694. http://dx.doi.Org/10.1016/j.topol.2011.10.016 Google Scholar
[25] Medvedev, S. V., About closed subsets of spaces of first category. Topology Appl. 159 (2012), no. 8, 2187–2192. http://dx.doi.Org/10.1016/j.topol.2012.02.012 Google Scholar
[26] Medvedev, S. V., Metrizable DH-spaces of the first category. Topology Appl. 179 (2015), 171–178. http://dx.doi.Org/10.1016/j.topol.2014.08.025 Google Scholar
[27] Miller, A. W, Special subsets of the real line. In: Handbook of set-theoretic topology, North-Holland, Amsterdam, 1984, pp. 201–233.Google Scholar
[28] Miller, A. W, Descriptive set theory and forcing. Lecture Notes in Logic, 4, Springer-Verlag, Berlin, 1995.Google Scholar
[29] Ostrovskii, A. V., On a question ofL. V. Keldysh on the structure ofBorel sets. Mat. Sb. (N.S.) 131 (173)(1986), no. 3, 323–346, 414 (in Russian); English translation in: Math. USSR-Sb 59 (1988), no. 2, 317–337.Google Scholar
[30] Terada, T., Spaces whose all nonempty clopen subsets are homeomorphic. Yokohama Math. J. 40 (1993), no. 2, 87–93.Google Scholar
[31] van Engelen, F., On the homogeneity of infinite products. Topology Proc. 17 (1992), 303–315.Google Scholar
[32] van Mill, J., The infinite-dimensional topology of function spaces. North-Holland Mathematical Library, 64, North-Holland Publishing Co., Amsterdam, 2001.Google Scholar
[33] van Mill, J., Characterization of some zero-dimensional separable metric spaces. Trans. Amer. Math. Soc. 264 (1981), no. 1, 205–215. http://dx.doi.org/10.1090/S0002-9947-1981-0597877-9 Google Scholar
[34] von Neumann, J., Characterisierung des Spektrums eines Integral-operators. Hermann, Paris, 1935.Google Scholar
[35] Yorke, J. A., Permutations and two sequences with the same cluster set. Proc. Amer. Math. Soc. 20 (1969), 606. Google Scholar