Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T01:01:51.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Countable Amenable Identity Excluding Groups

Published online by Cambridge University Press:  20 November 2018

Wojciech Jaworski
Wojciech Jaworski*
Affiliation:
School of Mathematics and Statistics Carleton University Ottawa, Ontario K1S 5B6, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A discrete group $G$ is called identity excluding if the only irreducible unitary representation of $G$ which weakly contains the 1-dimensional identity representation is the 1-dimensional identity representation itself. Given a unitary representation 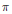$\pi $ of $G$ and a probability measure 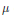$\mu $ on $G$, let 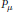${{P}_{\mu }}$ denote the 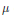$\mu $-average 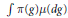$\int{\pi (g)\mu (dg)}$. The goal of this article is twofold: (1) to study the asymptotic behaviour of the powers 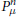$P_{\mu }^{n}$, and (2) to provide a characterization of countable amenable identity excluding groups. We prove that for every adapted probability measure 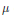$\mu $ on an identity excluding group and every unitary representation 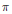$\pi $ there exists and orthogonal projection 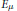${{E}_{\mu }}$ onto a 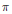$\pi $-invariant subspace such that 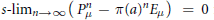$s-{{\lim }_{n\to \infty }}\,(P_{\mu }^{n}\,-\,\pi {{(a)}^{n}}\,{{E}_{\mu }})\,\,=\,0$ for every 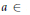$a\,\in $ supp 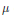$\mu $. This also remains true for suitably defined identity excluding locally compact groups. We show that the class of countable amenable identity excluding groups coincides with the class of 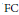$\text{FC}$-hypercentral groups; in the finitely generated case this is precisely the class of groups of polynomial growth. We also establish that every adapted random walk on a countable amenable identity excluding group is ergodic.

Keywords

22D1022D4043A0547A3560B1560J50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 2 , 01 June 2004 , pp. 215 - 228
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Akcoglu, M. A. and Boivin, D., Approximation of Lp-contractions by isometries. Canad. Math. Bull. 32 (1989), 360–364.Google Scholar
[2] Azencott, R., Espaces de Poisson des groupes localement compacts. In: Lecture Notes in Math. 148, Springer, New York, 1970.Google Scholar
[3] Bellow, A., Jones, R., and Rosenblatt, J., Almost everywhere convergence of weighted averages. Math. Ann. 293 (1992), 399–426.Google Scholar
[4] Bellow, A., Jones, R., and Rosenblatt, J., Almost everywhere convergence of convolution powers. Ergodic Theory Dynam. Systems 14 (1994), 415–432.Google Scholar
[5] Bellow, A., Jones, R., and Rosenblatt, J., Almost everywhere convergence of powers. Almost everywhere convergence, (eds., G. A. Edgar and L. Sucheston), Proceedings of the International Conference on Almost Everywhere Convergence in Probability and Ergodic Theory, Ohio State Univ., 1988, Academic Press, New York, 1989, 99–120.Google Scholar
[6] Derriennic, Y. and Lin, M., Convergence of iterates of averages of certain operator representations and of convolution powers. J. Funct. Anal. 85 (1989), 86–102.Google Scholar
[7] Dixmier, J., C*-algebras. North-Holland, Amsterdam, 1977.Google Scholar
[8] Duguid, A. M. and McLain, D. H., FC-nilpotent and FC-soluble groups. Proc. Cambridge Philos. Soc. 52 (1956), 391–398.Google Scholar
[9] Gromov, M., Groups of polynomial growth and expanding maps. Inst. Hautes É tudes Sci. Publ. Math. 53 (1981), 53–73.Google Scholar
[10] Hewitt, E. and Ross, K., Abstract Harmonic Analysis, Vol. I. 2nd ed., Springer, New York, 1979.Google Scholar
[11] Jaworski, W., Strongly approximately transitive group actions, the Choquet-Deny theorem, and polynomial growth. Pacific J. Math. 165 (1994), 115–129.Google Scholar
[12] Jaworski, W., Exponential boundedness and amenability of open subsemigroups of locally compact groups. Canad. J. Math. 46 (1994), 1263–1274.Google Scholar
[13] Jaworski, W., Rosenblatt, J., and Willis, G., Concentration functions in locally compact groups. Math. Ann. 305 (1996), 673–691.Google Scholar
[14] Jones, R., Rosenblatt, J. and Tempelman, A., Ergodic theorems for convolutions of a measure on a group. Illinois J. Math. 38 (1994), 521–553.Google Scholar
[15] Kaimanovich, V. A. and Vershik, A. M., Random walk on discrete groups: boundary and entropy. Ann. Probab. 11 (1983), 457–490.Google Scholar
[16] Lin, M. and Wittmann, R., Convergence of representation averages and of convolution powers. Israel J. Math. 88 (1994), 125–127.Google Scholar
[17] Lin, M. and Wittmann, R., Averages of unitary representations and weak mixing of random walks. Studia Math. 114 (1995), 127–145.Google Scholar
[18] McLain, D. H., Remarks on the upper central series of a group. Proc. Glasgow Math. Assoc. 3 (1956), 38–44.Google Scholar
[19] Raja, C. R. E., Weak mixing and unitary representation problem. Bull. Sci.Math. 124 (2000), 517–523.Google Scholar
[20] Raja, C. R. E., Identity excluding groups. 16 pages, preprint.Google Scholar
[21] Revuz, D., Markov Chains. North Holland, Amsterdam, 1984.Google Scholar
[22] Robinson, D. J. S., Finiteness Conditions in Generalized Soluble Groups, Part 1. Springer, Berlin, 1972.Google Scholar
[23] Rosenblatt, J., Ergodic and mixing random walks on locally compact groups. Math. Ann. 257 (1981), 31–42.Google Scholar
[24] Rosenblatt, J., Ergodic groups actions. Arch. Math. 47 (1986), 263–269.Google Scholar
[25] Tempelman, A. A., Ergodic theorems for group actions. Kluwer, New York, 1992.Google Scholar
[26] Yoshizawa, H., On unitary representations of the free group. Osaka Math. J. 3 (1951), 55–63.Google Scholar