Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T18:49:13.503Z Has data issue: false hasContentIssue false
  • English
  • Français

Correction to a Theorem on Total Positivity

Published online by Cambridge University Press:  20 November 2018

Carl Johan Ragnarsson ,
Wesley Wai Suen  and
David G. Wagner
Carl Johan Ragnarsson
Affiliation:
Pålsjövägen 16, SE-22363 Lund, Sweden e-mail: [email protected]
Wesley Wai Suen
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail: [email protected]@math.uwaterloo.ca
David G. Wagner
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail: [email protected]@math.uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A well-known theorem states that if 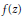$f\left( z \right)$ generates a 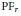$\text{P}{{\text{F}}_{r}}$ sequence then 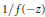$1/f\left( -z \right)$ generates a 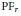$\text{P}{{\text{F}}_{r}}$ sequence. We give two counterexamples which show that this is not true, and give a correct version of the theorem. In the infinite limit the result is sound: if 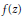$f\left( z \right)$ generates a 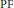$\text{PF}$ sequence then 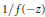$1/f\left( -z \right)$ generates a 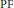$\text{PF}$ sequence.

Keywords

15A4815A4515A5705E05Total positivityToeplitz matrixPólya frequency sequenceskew Schur function
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 2 , 01 June 2006 , pp. 281 - 284
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Aissen, M., Schoenberg, I. J., and Whitney, A., On the generating functions of totally positive sequences. Proc. Nat. Acad. Sci. U.S.A. 37(1952), 303–307.Google Scholar
[2] Karlin, S., Total Positivity, I. Stanford University Press, Stanford, CA, 1968.Google Scholar
[3] Macdonald, I. G., Symmetric Functions and Hall Polynomials. Second edition. Oxford University Press, Oxford, 1995.Google Scholar
[4] Schoenberg, I. J., On smoothing operations and their generating functions. Bull. Amer. Math. Soc. 59(1953), 199–230.Google Scholar
[5] Schoenberg, I. J., On the zeros of the generating functions of multiply positive sequences and functions. Ann. of Math. 62(1955), 447–471.Google Scholar