Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Pagter, B
and
Schep, A.R
1988.
Measures of non-compactness of operators in Banach lattices.
Journal of Functional Analysis,
Vol. 78,
Issue. 1,
p.
31.
Gutek, A
Hart, D
Jamison, J
and
Rajagopalan, M
1991.
Shift operators on Banach spaces.
Journal of Functional Analysis,
Vol. 101,
Issue. 1,
p.
97.
1993.
Composition Operators on Function Spaces.
Vol. 179,
Issue. ,
p.
273.
Jabbarzadeh, M. R.
and
Estaremi, Y.
2012.
Essential norm of substitution operators on L p spaces.
Indian Journal of Pure and Applied Mathematics,
Vol. 43,
Issue. 3,
p.
263.
LO, CHING-ON
and
LOH, ANTHONY WAI-KEUNG
2021.
WEIGHTED COMPOSITION OPERATORS BETWEEN LORENTZ SPACES.
Bulletin of the Australian Mathematical Society,
Vol. 103,
Issue. 3,
p.
493.


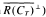 is either zero or infinite. As a corollary, when m has no atoms,
is either zero or infinite. As a corollary, when m has no atoms, 