Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T13:43:19.853Z Has data issue: false hasContentIssue false
  • English
  • Français

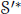Convolution Equation in —Propagation of Singularities

Published online by Cambridge University Press:  20 November 2018

Stevan Pilipović
Stevan Pilipović*
Affiliation:
Institute of Mathematics University of Novi Sad Trg Dositeja Obradovića 4 21000 Novi Sad Yugoslavia, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

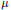The singular spectrum of $u$ in a convolution equation $\mu *u\,=\,f$, where $\mu$ and 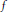$f$ are tempered ultra distributions of Beurling or Roumieau type is estimated by

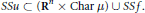$$SSu\,\subset \,\left( {{\mathbf{R}}^{n}}\,\times \,\text{Char}\,\mu \right)\,\cup \,SSf$$

The same is done for 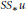$S{{S}_{*}}u$.

Keywords

32A4046F1558G07
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 1 , 01 March 2001 , pp. 105 - 114
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Dong, C. and Matsuzawa, T., S-spaces of Gel’fand-Shilov and differential equations. Japan. J. Math. (2) 19 (1994), 227–239.Google Scholar
[2] Eida, A. and Pilipović, , On the microlocal decomposition of some classes of hyperfunctions. Math. Proc. Cambridge Philos. Soc. 125 (1999), 455–461.Google Scholar
[3] Floret, K. and Wloka, J., Einfürung in die Theorie der lokalkonvexen Räume. Springer, Lecture Notes in Math. 59, Berlin, Heidelberg, New York, 1968.Google Scholar
[4] Hörmander, L., The Analysis of Linear Partial Differential Operators I. Springer, Berlin, Heidelberg, New York, Tokyo, 1983.Google Scholar
[5] Komatsu, H., Ultradistributions, I–III. J. Fac. Sci. Univ. Tokyo Sect. IAMath. 20 (1973), 25–105; 24 (1977), 607–0628; 29 (1982), 653–717.Google Scholar
[6] Komatsu, H.,Microlocal Analytic in Gevrey Classes and in Convex Domains. Springer, Lecture Notes in Math. 1726, 1989, 426–493.Google Scholar
[7] Kovačević, D. and Pilipović, S., Structural properties of the space of tempered ultradistributions. Proc. Conf., Comp. Analysis and Generalized Functions, Varna, 1991, 1993, 169–184.Google Scholar
[8] Petzsche, H. J., Generalized functions and the boundary values of holomorphic functions. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 31 (1984), 391–431.Google Scholar
[9] Pilipović, S., Characterization of bounded sets in spaces of ultradistributions. Proc. Amer. Math. Soc. 120 (1994), 1191–1206.Google Scholar
[10] Pilipović, S., Microlocal Analysis of ultradistributions. Proc. Amer. Math. Soc. 126 (1998), 105–113.Google Scholar
[11] Rodino, L., Linear partial differential operators in Gevrey spaces. World Scientific, Singapore, 1993.Google Scholar
[12] de Roewer, J. W., Hyperfunctional singular support of distributions. J. Fac. Sci.Univ. Tokyo Sect. IA Math. 31 (1985), 585–631.Google Scholar
[13] Sato, M., Kawai, T. and Kashiwara, M., Microfunctions and Pseudo-differential Equations. Springer, Lecture Notes in Math. 287, 1973, 265–529.Google Scholar