Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T23:54:53.981Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence of Solutions of Third Order Differential Equations*

Published online by Cambridge University Press:  20 November 2018

K. E. Swick
K. E. Swick*
Affiliation:
Occidental College, Los Angeles, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a system of differential equations 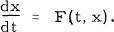. Solutions of this system are said to be convergent if, given any pair of solutions x(t), y(t), x(t) - y(t) → 0 as t → ∞. In this case the system is also said to be extremely stable.

In [6] a technique was developed which yielded the convergence of solutions of the forced Lienard equation. Here a similar technique i s applied to forced third order equations. A critical step in [6] was to show that a certain matrix was negative definite. This could be done directly in [6] since the matrix was only 2 × 2. With third and higher order equations, direct use of necessary and sufficient conditions is not feasible since the computations become unwieldy.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 6 , December 1969 , pp. 779 - 792
Copyright
Copyright © Canadian Mathematical Society 1969

Footnotes

This work was supported in part by National Science Foundation COSIP (GY 4754).

*

Much of this paper is a part of the author's Ph. D. dissertation at the University of Iowa. The author wishes to thank Professor P.E. Waltman for his advice and encouragement.

References

1. Ezeilo, J. O. C., A note on the convergence of solutions of certain second order differential equations. Port. Math. 24 (1965) 49–58.Google Scholar
2. Fan, Ky, Inequalities for eigenvalues of Hermitian matrices. U.S. Department of Commerce, National Bureau of Standards, Appl. Math. Ser. 39, 131–139.Google Scholar
3. La Salle, J. P., A study of synchronous asymptotic stability. Ann. Math. 65 (1957) 571–581.Google Scholar
4. Lim, Y.S. and Kazda, L. F., A study of second order non-linear systems. J. Math. Anal, and Appl. 8 (1964) 423–444.Google Scholar
5. Marcus, M. and Mine, H., Introduction to linear algebra. (New York, 1965).Google Scholar
6. Waltman, P. and Bridgland, T. F. Jr, On convergence of solutions of the forced Iienard equation. J. Math, and Phys. 44 (1965) 284–287.Google Scholar