Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T11:58:29.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Construction of Special Edge-Chromatic Graphs

Published online by Cambridge University Press:  20 November 2018

J. G. Kalbfleisch
J. G. Kalbfleisch*
Affiliation:
University of Waterloo
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

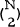The configuration formed by N points in general position in space, together with the lines joining them in pairs will be called an N-clique. The N-clique is coloured by assigning to each edge exactly one colour from a set of t possible colours. A theorem due to Ramsey [4] ensures the existence of a least integer M(q1, q2, …, qt) such that if N ≥ M, any such colouring of the N-clique must contain either a q1-clique entirely of colour 1, or a q2-clique of colour 2, …, or a qt-clique of colour t. Another proof of Ramsey's theorem is given by Ryser [5].

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 8 , Issue 5 , October 1965 , pp. 575 - 584
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Erdȍs, P. and Rogers, C. A., The Construction of Certain Graphs. Can. J. Math., 14 (1962), 702-707.Google Scholar
2. Erdȍs, P. and Szekeres, G., A Combinatorial Problem in Geometry. Compositio Math. 2 (1935), 463-470.Google Scholar
3. Greenwood, R.E. and Gleason, A.M., Combinatorial Relations and Chromatic Graphs. Can. J. Math. 7 (1955), 1-7.Google Scholar
4. Ramsey, F.P., On a Problem of Formal Logic. Proc. London Math. Soc., 2nd series,30 (1930), 264-286.Google Scholar
5. Ryser, H.J., Combinatorial Mathematics. Carus Math. Monograph 14 (1963), Ch. IV, 38-43.Google Scholar