Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T17:55:11.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Consecutive Integers with Close Kernels

Part of: Multiplicative number theory Elementary number theory

Published online by Cambridge University Press:  24 October 2018

Jean-Marie De Koninck  and
Florian Luca
Jean-Marie De Koninck
Affiliation:
Département de mathématiques et de statistique, Université Laval, Québec G1V 0A6, Canada Email: [email protected]
Florian Luca
Affiliation:
School of Mathematics, University of the Witwatersrand, Private Bag 3, Wits 2050, Johannesburg, South Africa Department of Mathematics, Faculty of Sciences, University of Ostrava, 30 Dubna 22, 701 03 Ostrava 1, Czech Republic Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

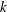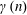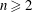Let $k$ be an arbitrary positive integer and let $\unicode[STIX]{x1D6FE}(n)$ stand for the product of the distinct prime factors of $n$. For each integer $n\geqslant 2$, let 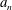$a_{n}$ and 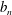$b_{n}$ stand respectively for the maximum and the minimum of the 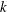$k$ integers 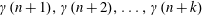$\unicode[STIX]{x1D6FE}(n+1),\unicode[STIX]{x1D6FE}(n+2),\ldots ,\unicode[STIX]{x1D6FE}(n+k)$. We show that 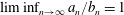$\liminf _{n\rightarrow \infty }a_{n}/b_{n}=1$. We also prove that the same result holds in the case of the Euler function and the sum of the divisors function, as well as the functions 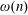$\unicode[STIX]{x1D714}(n)$ and 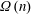$\unicode[STIX]{x1D6FA}(n)$, which stand respectively for the number of distinct prime factors of $n$ and the total number of prime factors of $n$ counting their multiplicity.

Keywords

arithmetic functionlocal behavior

MSC classification

Primary: 11A25: Arithmetic functions; related numbers; inversion formulas
Secondary: 11N64: Other results on the distribution of values or the characterization of arithmetic functions
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 3 , September 2019 , pp. 469 - 473
Copyright
© Canadian Mathematical Society 2018 

Footnotes

The work of the first author was supported in part by a grant from NSERC of Canada. The work of the second author was supported in part by grant CPRR160325161141 and an A-rated scientist award, both from the NRF of South Africa, and by grant no. 17-02804S of the Czech Granting Agency.

References

De Koninck, J. M., Friedlander, J., and Luca, F., On Strings of Consecutive Integers with a Distinct Number of Prime Factors . Proc. Amer. Math. Soc. 137(2009), 1585–1592.Google Scholar
De Koninck, J. M. and Luca, F., Analytic Number Theory: Exploring the Anatomy of Integers . Grad. Stud. in Math., Vol. 134, American Mathematical Society, 2012.Google Scholar
De Koninck, J. M. and Luca, F., Arithmetic functions monotonic at consecutive arguments . Stud. Sci. Math. Hung. 51(2014), 155–164.Google Scholar