Published online by Cambridge University Press: 20 November 2018
By applying the Cayley–Dickson process to the division algebra of real octonions, one obtains a 16-dimensional real algebra known as (real) sedenions. We denote this algebra by 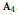 ${{\text{A}}_{4}}$. It is a flexible quadratic algebra (with unit element 1) but not a division algebra.
${{\text{A}}_{4}}$. It is a flexible quadratic algebra (with unit element 1) but not a division algebra.
We classify the subalgebras of 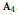 ${{\text{A}}_{4}}$ up to conjugacy (i.e., up to the action of the automorphism group
${{\text{A}}_{4}}$ up to conjugacy (i.e., up to the action of the automorphism group  $G$ of
$G$ of 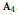 ${{\text{A}}_{4}}$) with one exception: we leave aside the more complicated case of classifying the quaternion subalgebras. Any nonzero subalgebra contains 1 and we show that there are no proper subalgebras of dimension 5, 7 or > 8. The proper non-division subalgebras have dimensions 3, 6 and 8. We show that in each of these dimensions there is exactly one conjugacy class of such subalgebras. There are infinitely many conjugacy classes of subalgebras in dimensions 2 and 4, but only 4 conjugacy classes in dimension 8.
${{\text{A}}_{4}}$) with one exception: we leave aside the more complicated case of classifying the quaternion subalgebras. Any nonzero subalgebra contains 1 and we show that there are no proper subalgebras of dimension 5, 7 or > 8. The proper non-division subalgebras have dimensions 3, 6 and 8. We show that in each of these dimensions there is exactly one conjugacy class of such subalgebras. There are infinitely many conjugacy classes of subalgebras in dimensions 2 and 4, but only 4 conjugacy classes in dimension 8.