Article contents
Conjugacy Classes and Binary Quadratic Forms for the Hecke Groups
Published online by Cambridge University Press: 20 November 2018
Abstract.
In this paper we give a lower bound with respect to block length for the trace of non-elliptic conjugacy classes of the Hecke groups. One consequence of our bound is that there are finitely many conjugacy classes of a given trace in anyHecke group. We show that another consequence of our bound is that class numbers are finite for related hyperbolic 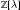 $\mathbb{Z}\left[ \text{ }\!\!\lambda\!\!\text{ } \right]$-binary quadratic forms. We give canonical class representatives and calculate class numbers for some classes of hyperbolic
$\mathbb{Z}\left[ \text{ }\!\!\lambda\!\!\text{ } \right]$-binary quadratic forms. We give canonical class representatives and calculate class numbers for some classes of hyperbolic 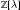 $\mathbb{Z}\left[ \text{ }\!\!\lambda\!\!\text{ } \right]$-binary quadratic forms.
$\mathbb{Z}\left[ \text{ }\!\!\lambda\!\!\text{ } \right]$-binary quadratic forms.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 2
- Cited by


