Published online by Cambridge University Press: 20 November 2018
A sequence {un}, n=0, 1, 2, 3,… is said to be an integral recurrence of order r if the terms satisfy the equation
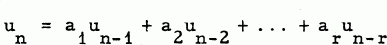
for n=r+1, r+2,…, and a1, a2,…, ar are integers, ar≠0. In this case we will say that {un} satisfies the relation [a1, a2,…, ar]. The sequence {un} is uniquely determined when u1, u2,…, ur are given specified values. If u1, u2,…, ur are integers all the terms of {un} are integers. The generating function f(t)=u1t + u2t2+… takes on the form 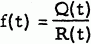 where Q(t) depends on the values of u1, u2,…, ur and R(t)=tr-a1tr-1-a2tr-2-…-ar. We will refer to R(t) as the characteristic polynomial of the recurrence.
where Q(t) depends on the values of u1, u2,…, ur and R(t)=tr-a1tr-1-a2tr-2-…-ar. We will refer to R(t) as the characteristic polynomial of the recurrence.