Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T00:14:26.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Condensed and Strongly Condensed Domains

Published online by Cambridge University Press:  20 November 2018

Abdeslam Mimouni
Abdeslam Mimouni*
Affiliation:
Department of Mathematical Sciences, King Fahd University of Petroleum and Minerals, Dhahran 31261, Saudi Arabia. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with the concepts of condensed and strongly condensed domains. By definition, an integral domain $R$ is condensed (resp. strongly condensed) if each pair of ideals 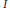$I$ and 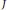$J$ of $R$, 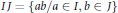$IJ\,=\,\{ab/a\,\in \,I,\,b\,\in \,J\}$ (resp. 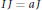$IJ\,=\,aJ$ for some 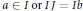$a\,\in \,I\,or\,I\,J\,=\,Ib$ for some 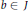$b\,\in \,J$). More precisely, we investigate the ideal theory of condensed and strongly condensed domains in Noetherian-like settings, especially Mori and strong Mori domains and the transfer of these concepts to pullbacks.

Keywords

13G0513A1513F0513E05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 3 , 01 September 2008 , pp. 406 - 412
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Anderson, D. D., Star-operations induced by overrings. Comm. Algebra 16(1988), no. 12, 2535–2553.Google Scholar
[2] Anderson, D. D. and Dumetriscu, T., Condensed domains. Canad. Math. Bull. 46(2003), no. 1, 3–13.Google Scholar
[3] Anderson, D. D. and Dumetriscu, T., Condensed local domains which are not strongly condensed. Math. Rep. 5(55)(2003), no. 3, 205–209.Google Scholar
[4] Anderson, D. F. and Dobbs, D. E., On the product of ideals. Canad. Math. Bull, 26(1983), no. 1, 106–114.Google Scholar
[5] Anderson, D. F., Arnold, J. T. and Dobbs, D. E., Integrally closed condensed domains are Bézout. Canad. Math. Bull, 28(1985), no. 1, 98–102.Google Scholar
[6] Barucci, V., Strongly divisorial ideals and complete integral closure of an integral domain. J. Algebra 99(1986), no. 1, 132–142.Google Scholar
[7] Barucci, V., Seminormal Mori domains. In: Commutative Ring Theory. Lecture Notes in Pure and Appl. Math. 153, Dekker, New York, 1994, pp. 163–170.Google Scholar
[8] Barucci, V., Mori domains. In: Non-Noetherian Commutative Ring Theory. Math. Appl. 520 Kluwer, Dordrecht, 2000, pp. 57–73.Google Scholar
[9] Barucci, V., Dobbs, D. E., and Fontana, M., Conducive integral domains as pullbacks. Manuscripta Math. 54(1986), no. 3, 261–277.Google Scholar
[10] Barucci, V., Gabelli, S., and Roitman, M., On semi-Krull domains. J. Algebra 145(1992), 306–328.Google Scholar
[11] Barucci, V. and Houston, E., On the prime spectrum of a Mori domain. Comm. Algebra, 24(1996), no. 11, 3599–3622.Google Scholar
[12] Bastida, E. and Gilmer, R., Overrings and divisorial ideals of rings of the form D + M. Michigan Math. J. 20(1973), 79–95.Google Scholar
[13] Brewer, J. W. and Rutter, E. A., D + M constructions with general overrings. Michigan Math. J. 23(1976), 33–42.Google Scholar
[14] Costa, D., Mott, J. L., and Zafrullah, M., The construction D + XDs[X]. J. Algebra 53(1978), no. 2, 423–439.Google Scholar
[15] Dobbs, D. E. and Fedder, R., Conducive integral domains. J. Algebra 86(1984), no. 2, 494–510.Google Scholar
[16] Dobbs, D. E., Houston, E. G., Lucas, T. G., and Zafrullah, M., t-linked overrings and Prüfer v-multiplication domains. Comm. Algebra 17(1989), no. 11, 2835–2852.Google Scholar
[17] Fanggui, W. and McCasland, R. L., On strong Mori domains. J. Pure Appl. Algebra 135(1999), no. 2, 155–165.Google Scholar
[18] Gabelli, S. and Houston, E., Coherentlike conditions in pullbacks. Michigan Math. J. 44(1997), no. 1, 99–123.Google Scholar
[19] Gilmer, R., Multiplicative Ideal Theory. Pure and Applied Mathematics 12, Marcel Dekker, New York, 1972.Google Scholar
[20] Gottlieb, C., On condensed Noetherian integral domains whose integral closures are discrete valuation rings. Canad. Math. Bull. 32(1989), no. 2, 166–168.Google Scholar
[21] Heinzer, W., Integral domains in which each non-zero ideal is divisorial. Mathematika 15(1968), 164–170.Google Scholar
[22] Houston, E. G. and Zafrullah, M., Integral domains in which each t-ideal is divisorial. Michigan. Math. J. 35(1988), no. 2, 291–300.Google Scholar
[23] Kaplansky, I., Commutative Rings. The University of Chicago Press, Chicago, 1974.Google Scholar
[24] Matlis, E., Some properties of commutative ring extensions. Illinois J. Math. 31(1987), no. 3, 374–418.Google Scholar
[25] Olberding, B., On the structure of stable domains. Comm. Algebra 30(2002), no. 2, 877–895.Google Scholar