No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
If 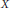 $X$ is a connected complex manifold with
$X$ is a connected complex manifold with 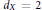 ${{d}_{X}}\,=\,2$ that admits a (connected) Lie group
${{d}_{X}}\,=\,2$ that admits a (connected) Lie group 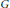 $G$ acting transitively as a group of holomorphic transformations, then the action extends to an action of the complexification
$G$ acting transitively as a group of holomorphic transformations, then the action extends to an action of the complexification 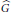 $\widehat{G}$ of
$\widehat{G}$ of 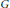 $G$ on
$G$ on 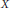 $X$ except when either the unit disk in the complex plane or a strictly pseudoconcave homogeneous complex manifold is the base or fiber of some homogeneous fibration of
$X$ except when either the unit disk in the complex plane or a strictly pseudoconcave homogeneous complex manifold is the base or fiber of some homogeneous fibration of 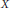 $X$.
$X$.