Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T18:57:41.371Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison Theorem for Conjugate Points of a Fourth-order Linear Differential Equation

Published online by Cambridge University Press:  20 November 2018

Jamel Ben Amara
Jamel Ben Amara*
Affiliation:
Faculté des Sciences de Bizerte, Tunisia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1961, J. Barrett showed that if the first conjugate point 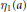${{\eta }_{1}}\left( a \right)$ exists for the differential equation 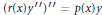${{\left( r\left( x \right){y}'' \right)}^{\prime \prime }}=p\left( x \right)y$, where 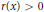$r\left( x \right)\,>\,0$ and 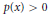$p\left( x \right)\,>\,0$, then so does the first systems-conjugate point 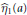${{\hat{\eta }}_{1}}\left( a \right)$. The aim of this note is to extend this result to the general equation with middle term 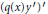${{\left( q\left( x \right){y}' \right)}^{\prime }}$ without further restriction on 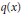$q\left( x \right)$, other than continuity.

Keywords

47E0534B0534C10fourth-order linear differential equationconjugate pointssystem-conjugate pointssubwronskians
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 1 , 01 March 2013 , pp. 39 - 43
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Banks, D. O. and Kurowski, G. J., A Prüfer transformation for the equation of a vibrating beam subject to axial forces. J. Differential Equations 24 (1977), no. 1, 57–74. http://dx.doi.org/10.1016/0022-0396(77)90170-X Google Scholar
[2] Barrett, J. H., Systems-disconjugacy of a fourth-order differential equations. Proc. Amer. Math. Soc. 12 (1961), 205–213.Google Scholar
[3] Barrett, J. H., Fourth order boundary value problems and comparison theorems. Canad. J. Math. 13 (1961), 625–638. http://dx.doi.org/10.4153/CJM-1961-051-x Google Scholar
[4] Ben Amara, , Oscillation criteria for fourth-order linear differential equations with middle term. Math. Nachr., to appear.Google Scholar
[5] Courant, R. and Hilbert, D., Equations of mathematical physics. Vol. I. Interscience Publishers, New York, 1953.Google Scholar
[6] Greenberg, L., An oscillation method for fourth-order, selfadjoint, two-point boundary value problems with nonlinear eigenvalues. SIAM J. Math. Anal. 22 (1991), no. 4, 1021–1042. http://dx.doi.org/10.1137/0522067 Google Scholar
[7] Hinton, D. B., Clamped end boundary conditions for fourth-order selfadjoint differential equations. Duke Math. J. 34 (1967), 131–138. http://dx.doi.org/10.1215/S0012-7094-67-03415-1 Google Scholar
[8] Leighton, W. and Nehari, Z., On the oscillation of solutions of self-adjoint linear differential equations of fourth order. Trans. Amer. Math. Soc. 98 (1958), 325–377. http://dx.doi.org/10.1090/S0002-9947-1958-0102639-X Google Scholar
[9] Lewis, R. T., The oscillation of fourth order linear differential equations. Canad. J. Math. 27 (1975), 138–145. http://dx.doi.org/10.4153/CJM-1975-017-4 Google Scholar
[10] Müller-Pfeiffer, , Oscillation criteria for selfadjoint fourth order differential equations. J. Differential Equations 46 (1982), no. 2, 194–215. http://dx.doi.org/10.1016/0022-0396(82)90115-2 Google Scholar
[11] Weinberger, H. F., Variational methods for eigenvalue approximation. Conference Board of the Mathematical Sciences Regional Conference Series in Applied Mathematics, 15, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1974.Google Scholar