Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-26T05:44:07.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact Operators in Regular LCQ Groups

Published online by Cambridge University Press:  20 November 2018

Mehrdad Kalantar
Mehrdad Kalantar*
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that a regular locally compact quantum group 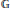$\mathbb{G}$ is discrete if and only if ${{\mathcal{L}}^{\infty }}\left( \mathbb{G} \right)$ contains non-zero compact operators on 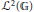${{\mathcal{L}}^{2}}\left( \mathbb{G} \right)$. As a corollary we classify all discrete quantum groups among regular locally compact quantum groups 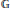$\mathbb{G}$ where 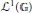${{\mathcal{L}}^{1}}\left( \mathbb{G} \right)$ has the Radon-Nikodym property.

Keywords

46L89locally compact quantum groupsregularitycompact operators
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 3 , 01 September 2014 , pp. 546 - 550
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Baaj, S. and Skandalis, G., Unitaires multiplicatifs et dualit´e pour les produits crois´es de C*-algçbres. Ann. Sci. Ecole Norm. Sup. 26 (1993), 425–488.Google Scholar
[2] Diestel, J. and Uhl, J. Jr., Vector Measures. American Mathematical Society, Providence, RI, 1977.Google Scholar
[3] Hu, Z., Neufang, M. and Ruan, Z.-J., Convolution of trace class operators over locally compact quantum groups. Canad. J. Math. Published online September 10, 2012; to appear in print. http://dx.doi.org/10.4153/CJM-2012-030-5 Google Scholar
[4] Kustermans, J. and Vaes, S., Locally compact quantum groups. Ann. Sci. Ecole Norm. Sup. 33 (2000), 837–934.Google Scholar
[5] Runde, V., Characterizations of compact and discrete quantum groups through second duals. J. Operator Theory 60 (2008), 415–428.Google Scholar
[6] Taylor, K. F., Geometry of the Fourier algebras and locally compact groups with atomic unitary representations. Math. Ann. 262 (1983), 183–190. http://dx.doi.org/10.1007/BF01455310 Google Scholar
[7] Woronowicz, S. L., Compact quantum groups. In: Symétries quantiques (Les Houches, 1995), North-Holland, Amsterdam, 1998, 845–884.Google Scholar