Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T17:31:05.450Z Has data issue: false hasContentIssue false
  • English
  • Français

A Common Generalization of Functional Equations Characterizing Normed and Quasi-Inner-Product Spaces

Published online by Cambridge University Press:  20 November 2018

B. R. Ebanks ,
PL. Kannappan  and
P. K. Sahoo
B. R. Ebanks
Affiliation:
Department of Mathematics University of Louisville Louisville, Kentucky 40292 U.S.A.
PL. Kannappan
Affiliation:
Department of Pure Mathematics University of Waterloo Waterloo, Ontario N2L 3G1
P. K. Sahoo
Affiliation:
Department of Mathematics University of Louisville Louisville, Kentucky 40292 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

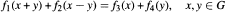We determine the general solutions of the functional equation for ƒi: G → F (i = 1,2,3,4), where G is a 2-divisible group and F is a commutative field of characteristic different from 2. The motivation for studying this equation came from a result due to Dry gas [4] where he proved a Jordan and von Neumann type characterization theorem for quasi-inner products. Also, this equation is a generalization of the quadratic functional equation investigated by several authors in connection with inner product spaces and their generalizations. Special cases of this equation include the Cauchy equation, the Jensen equation, the Pexider equation and many more. Here, we determine the general solution of this equation without any regularity assumptions on ƒi.

Keywords

39B4039B5046C10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 3 , 01 September 1992 , pp. 321 - 327
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Aczel, J., Chung, J. K. and Ng, C. T., Symmetric second differences in product form on groups , In: Topics in Mathematical Analysis, (éd. Th. M. Rassias), World Scientific Publ. Co. (1989), 1–22.Google Scholar
2. Aczel, J. and Dhombres, J., Functional equations in several variables , Cambridge University Press, Cambridge, 1989.Google Scholar
3. Dhombres, J., Some aspects of functional equations. Chulalongkorn University Press, Bangkok, 1979.Google Scholar
4. Drygas, H., Quasi-inner products and their applications , In: Advances in Multivariate Statistical Analysis, (ed. A. K. Gupta), D. Reidel Publishing Co. (1987), 13–30.Google Scholar
5. Kurepa, S., On the Junctional equation:T1 (t+s)T2(t-s) = T3(t)T4(s), Publ. Inst. Math. (Beograd) 16(1962), 99–108.Google Scholar
6. Vajzović, F., On the Junctional equation: T1(t + s)T2(t - s) = T3(t)T4(s), Publ. Inst. Math. (Beograd) 18(1964), 21–27.Google Scholar