Let $A$ be a Banach algebra and let 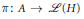$\pi :\,A\,\to \,\mathcal{L}\left( H \right)$ be a continuous representation of $A$ on a separable Hilbert space $H$ with dim 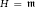$H\,=\,\text{m}$. Let 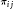${{\pi }_{ij}}$ be the coordinate functions of $\pi $ with respect to an orthonormal basis and suppose that for each 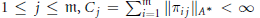$1\,\le \,j\,\le \,\text{m,}\,{{C}_{j}}\,=\,\sum\nolimits_{i=1}^{\text{m}}{\left\| {{\pi }_{ij}} \right\|}{{A}^{*}}\,<\,\infty $ and 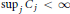${{\sup }_{j}}\,{{C}_{j}}\,<\,\infty $. Under these conditions, we call an element 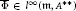$\overline{\Phi }\,\in \,{{\iota }^{\infty }}\,\left( \mathfrak{m},\,{{A}^{**}} \right)$ left $\pi $-invariant if 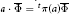$a\,\cdot \overline{\Phi }\,={{\,}^{^{t}\pi }}\left( a \right)\overline{\Phi }$ for all 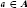$a\in A$ In this paper we prove a link between the existence of left $\pi $-invariant elements and the vanishing of certain Hochschild cohomology groups of $A$. Our results extend an earlier result by Lau on $F$-algebras and recent results of Kaniuth, Lau, Pym, and and the second author in the special case where 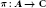$\pi :\,A\,\to \text{C}$ is a non-zero character on $A$.