Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-25T04:06:29.426Z Has data issue: false hasContentIssue false
  • English
  • Français

The Co-annihilating-ideal Graphs of Commutative Rings

Published online by Cambridge University Press:  20 November 2018

Saeeid Akbari ,
Abbas Alilou ,
Jafar Amjadi  and
Seyed Mahmoud Sheikholeslami
Saeeid Akbari
Affiliation:
Department of Mathematical Sciences, Sharif University of Technology, Tehran, I. R. Iran e-mail: [email protected] e-mail: [email protected]
Abbas Alilou
Affiliation:
Department of Mathematics, Azarbaijan Shahid Madani University, Tabriz, I.R. Iran e-mail: [email protected] e-mail: [email protected]
Jafar Amjadi
Affiliation:
Department of Mathematics, Azarbaijan Shahid Madani University, Tabriz, I.R. Iran e-mail: [email protected] e-mail: [email protected]
Seyed Mahmoud Sheikholeslami
Affiliation:
Department of Mathematics, Azarbaijan Shahid Madani University, Tabriz, I.R. Iran e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

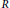Let $R$ be a commutative ring with identity. The co-annihilating-ideal graph of 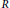$R$, denoted by 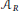${{\mathcal{A}}_{R}}$, is a graph whose vertex set is the set of all non-zero proper ideals of 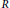$R$ and two distinct vertices $I$ and 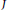$J$ are adjacent whenever 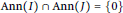$\text{Ann}\left( I \right)\,\cap \,\text{Ann}\left( J \right)\,=\,\left\{ 0 \right\}$. In this paper we initiate the study of the co-annihilating ideal graph of a commutative ring and we investigate its properties.

Keywords

13A1516N40commutative ringco-annihilating-ideal graph
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 3 - 11
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Aalipour, G., Akbari, S., Behboodi, M., Nikandish, R.,Nikmehr, M. J., and Shaveisi, F., The classification of the annihilating-ideal graph of a commutative ring. Algebra Colloq. 21(2014), 249–256. http://dx.doi.Org/10.1142/S1005386714000200 Google Scholar
[2] Aalipour, G., Akbari, S., Nikandish, R.,Nikmehr, M. J., and Shaveisi, E., Minimal prime ideals and cycles in annihilating-ideal graph. Rocky Mountain J. Math. 43(2013), 1415–1425. http://dx.doi.Org/10.1216/RMJ-2O13-43-5-1415 Google Scholar
[3] Aalipour, G., Akbari, S., Nikandish, R.,Nikmehr, M. J., and Shaveisi, E., On the coloring of the annihilating-ideal graph of a commutative ring. Discrete Math. 312(2012), 2620–2626. http://dx.doi.Org/10.1016/j.disc.2011.10.020 Google Scholar
[4] Aliniaeifard, F., Behboodi, M., Mehdi-Nezhad, E., and Rahimi, A.M., The annihilating-ideal graph of a commutative ring with respect to an ideal. Comm. Algebra 42(2014), 2269–2284. http://dx.doi.Org/10.1080/00927872.2012.753606 Google Scholar
[5] Akbari, S., Maimani, H.R., and Yassemi, S., When a zero-divisor graph is planar or a complete r-partitegraph. J. Algebra 270(2003), 169–180. http://dx.doi.Org/10.1016/S0021-8693(03)00370-3 Google Scholar
[6] Akbari, S. and Mohammadian, A., Zero-divisor graphs of non-commutative rings. J. Algebra 296(2006), 462–479. http://dx.doi.Org/10.1016/j.jalgebra.2005.07.007 Google Scholar
[7] Anderson, D. D. and Naseer, M., Beck's coloring of a commutative ring. J. Algebra 159(1993), 500–514. http://dx.doi.Org/10.1006/jabr.1993.1171 Google Scholar
[8] Anderson, D. D. and Mulay, S. B., On the diameter and girth of a zero-divisor graph. J. Pure Appl. Algebra 210(2007), 543–550. http://dx.doi.Org/10.1016/j.jpaa.2006.10.007 Google Scholar
[9] Anderson, D. E. andLivingston, P. S., The zero-divisor graph of a commutative ring. J. Algebra 217(1999), 434–447. http://dx.doi.Org/10.1006/jabr.1998.7840 Google Scholar
[10] Atiyah, M. E. and Macdonald, I. G., Introduction to commutative algebra. Addison-Wesley, 1969.Google Scholar
[11] Beck, I., Coloring of commutative rings. J. Algebra 116(1988), 208–226. http://dx.doi.Org/10.1016/0021-8693(88)90202-5 Google Scholar
[12] Behboodi, M. and Rakeei, Z., The annihilating-ideal graph of commutative rings. I. J. Algebra Appl. 10(2011), 727–739. http://dx.doi.Org/!0.1142/S0219498811004896 Google Scholar
[13] Behboodi, M. and Rakeei, Z., The annihilating-ideal graph of commutative rings. II. J. Algebra Appl. 10(2011), 741–753. http://dx.doi.Org/10.1142/S0219498811004902 Google Scholar
[14] Chakrabarty, I., Ghosh, S.,Mukherjee, T. K., and Sen, M. K., Intersection graphs of ideals of rings. Discrete. Math. 309(2009), 5381–5392. http://dx.doi.Org/10.1016/j.disc.2008.11.034 Google Scholar
[15] Lu, D., Wu, T., Ye, M., and Yu, H., On graphs related to the co-maximal ideals of a commutative ring. ISRN Combinatorics Volume 2013, Article ID 354696, 7 pages.Google Scholar
[16] Lucas, T. G., The diameter of a zero divisor graph. J. Algebra 301(2006), 174–193. http://dx.doi.Org/10.101 6/j.jalgebra.2006.01.01 9 Google Scholar
[17] Lam, T.Y., A first course in non-commutative rings. Springer-Verlag, New York, 1991.Google Scholar
[18] Matlis, E., The minimal prime spectrum of a reduced ring. Illinois J. Math. 27(1983), 353–391.Google Scholar
[19] Samei, K., On the comaximal graph of a commutative ring. Canad. Math. Bull. 57(2014), 413–423. http://dx.doi.Org/10.4153/CMB-2013-033-7.Google Scholar
[20] West, D. B., Introduction to graph theory. Second edition. Prentice Hall, USA, 2001.Google Scholar