Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T10:03:47.372Z Has data issue: false hasContentIssue false
  • English
  • Français

The Classification of Pin4-Bundles over a 4-Complex

Published online by Cambridge University Press:  20 November 2018

Christian Weber
Christian Weber*
Affiliation:
Max-Planck-Institut für Mathematik Gottfried-Claren-Straße 26 D-53225 Bonn Germany, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we show that the Lie-group 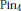$\text{Pi}{{\text{n}}_{4}}$ is isomorphic to the semidirect product 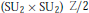$\text{(S}{{\text{U}}_{2}}\times \text{S}{{\text{U}}_{2}})\text{Z/2}$ where 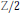$Z/2$ operates by flipping the factors. Using this structure theorem we prove a classification theorem for 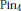$\text{Pi}{{\text{n}}_{4}}$-bundles over a finite 4-complex 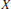$X$.

Keywords

55N2555R1057S15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 2 , 01 June 1999 , pp. 248 - 256
Copyright
Copyright © Canadian Mathematical Society 1999

References

[Bro82] Brown, Kenneth S., Cohomology of Groups. Graduate Texts in Math. 87, Springer-Verlag, New York, Heidelberg, Berlin, 1982.Google Scholar
[DW59] Dold, A. and Whitney, H., Classification of oriented sphere bundles over a 4-complex. Ann. of Math. (2) 69 (1959), 667–677.Google Scholar
[EM47] Eilenberg, S. and MacLane, S., Cohomology theory in abstract groups II. Ann. of Math. (2) 48 (1947), 326–41.Google Scholar
[HH58] Hirzebruch, F. and Hopf, H., Felder von Flächenelementen in 4-dimensionalenMannigfaltigkeiten.Math. Ann. 136 (1958), 156–172.Google Scholar
[LM89] Blaine Lawson, H. Jr. andMarie-LouiseMichelson, Spin Geometry. Princeton Math. Ser. 38, Princeton Univ. Press, Princeton, New Jersey, 1989.Google Scholar
[Web96] Weber, Christian, Gauge theory on nonorientable four-manifolds. Verlag (ed. Dr. Kovăc), Hamburg, 1996.Google Scholar