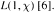Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T17:15:01.498Z Has data issue: false hasContentIssue false
  • English
  • Français

The Class Number Formula of a Real Quadratic Field and an Estimate of the Value of a Unit

Published online by Cambridge University Press:  20 November 2018

T. Mitsuhiro ,
T. Nakahara  and
T. Uehara
T. Mitsuhiro
Affiliation:
Graduate School of Science and Engineering, Saga University, Saga 840, Japan, e-mail:[email protected]
T. Nakahara
Affiliation:
Faculty of Science and Engineering, Saga University, Saga 840, Japan, e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our aim is to give an arithmetical expression of the class number formula of real quadratic fields. Starting from the classical Dirichlet class number formula, our proof goes along arithmetical lines not depending on any analytical method such as an estimate for

Keywords

11R2911R1111R18
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 38 , Issue 1 , 01 March 1995 , pp. 98 - 103
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Bergstrom, H., Die Klassenzahlformel für réelle quadratische Zahlkörper mit zusammengesetzer Diskriminante als Produkt verallgemeinerter Gaufischer Summen, J. Reine Angew. Math. 186(1945), 91–115.Google Scholar
2. Chowla, P., On the class-number of real quadratic fields, J. Reine Angew. Math. 230(1968), 51–60.Google Scholar
3. Chowla, P. and Chowla, S., Formulae for the units and class-numbers of real quadratic fields, J. Reine Angew. Math. 230(1968), 61–65.Google Scholar
4. Hasse, H., Vorlesungen Über Zahlentheorie, Springer Verlag, Berlin, Gôttingen, Heidelberg, New York, 1964.Google Scholar
5. Mitsuhiro, T., A combinatorial proof of an arithmetical expression of Dirichlet's class number formula, Rep. Fac. Sci. Engrg. Saga Univ. Math. 22(1993), 1–18.Google Scholar
6. Mitsuhiro, T. and Nakahara, T., An arithmetical expression of Dirichlet's class number formula, In: The Proceedings of Analytic Number Theory and Related Topics, World Scientific, Singapore, 1993, 97–107, Insertion of Tables, i-iv.Google Scholar
7. Ono, T., A deformation of Dirichlet's class number formula, In: Algebraic Analysis, Vol. II, (eds. Kashiwara, M. and Kawai, T.), Academic Press, Boston, 1988, 659–666.Google Scholar