Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schlaepfer, F.
and
Schweppe, F.
1972.
Continuous-time state estimation under disturbances bounded by convex sets.
IEEE Transactions on Automatic Control,
Vol. 17,
Issue. 2,
p.
197.
Fischer, Herbert
1975.
Interval Mathematics.
Vol. 29,
Issue. ,
p.
184.
Fogel, E.
and
Huang, Y.
1980.
Adaptive algorithms for non-stastical parameter estimation in linear models.
Vol. 5,
Issue. ,
p.
1022.
Chernousko, F. L.
1982.
Ellipsoidal bounds for sets of attainability and uncertainty in control problems.
Optimal Control Applications and Methods,
Vol. 3,
Issue. 2,
p.
187.
Fogel, Eli
and
Huang, Y.F.
1982.
On the value of information in system identification—Bounded noise case.
Automatica,
Vol. 18,
Issue. 2,
p.
229.
Fogel, E.
1982.
Membership Set Estimation – An Alternative Approach to System Identification.
IFAC Proceedings Volumes,
Vol. 15,
Issue. 4,
p.
709.
Kai-Bor Yu
1984.
An improved signal restoration method using frequency domain information.
Vol. 9,
Issue. ,
p.
116.
Pierce, Jane E.
and
Rust, Bert W.
1985.
Constrained Least Squares Interval Estimation.
SIAM Journal on Scientific and Statistical Computing,
Vol. 6,
Issue. 3,
p.
670.
Huang, Y.
1986.
A recursive estimation algorithm using selective updating for spectral analysis and adaptive signal processing.
IEEE Transactions on Acoustics, Speech, and Signal Processing,
Vol. 34,
Issue. 5,
p.
1331.
Nickel, K. L. E.
1986.
Using Interval Methods for the Numerical Solution of ODE's.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 66,
Issue. 11,
p.
513.
Pearson, Ronald K.
1988.
Block-Sequential Algorithms for Set-Theoretic Estimation.
SIAM Journal on Matrix Analysis and Applications,
Vol. 9,
Issue. 4,
p.
513.
Deller, J.R.
1989.
Set membership identification in digital signal processing.
IEEE ASSP Magazine,
Vol. 6,
Issue. 4,
p.
4.
Walter, Eric
and
Piet-Lahanier, Hélène
1990.
Estimation of parameter bounds from bounded-error data: a survey.
Mathematics and Computers in Simulation,
Vol. 32,
Issue. 5-6,
p.
449.
Veres, S.M.
and
Norton, J.P.
1991.
Adaptive pole-placement control using parameter bounds.
p.
2860.
Cheung, M.-F.
Yurkovich, S.
and
Passino, K.M.
1991.
An optimal volume ellipsoid algorithm for parameter set estimation.
p.
969.
Preciado, A.
Meizel, D.
Segovia, A.
and
Rombaut, M.
1991.
Fusion of multi-sensor data: a geometric approach.
p.
2806.
Neumaier, A.
1993.
Validation Numerics.
Vol. 9,
Issue. ,
p.
175.
Cheung, M.-F.
Yurkovich, S.
and
Passino, K.M.
1993.
An optimal volume ellipsoid algorithm for parameter set estimation.
IEEE Transactions on Automatic Control,
Vol. 38,
Issue. 8,
p.
1292.
Deller, J.R.
Nayeri, M.
and
Odeh, S.F.
1993.
Least-square identification with error bounds for real-time signal processing and control.
Proceedings of the IEEE,
Vol. 81,
Issue. 6,
p.
815.
Walter, E.
and
Pronzato, L.
1994.
Characterizing Sets Defined By Inequalities.
IFAC Proceedings Volumes,
Vol. 27,
Issue. 8,
p.
325.


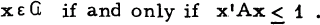
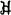 circumscribed about G
circumscribed about G if and only if x'hx ≤ max
if and only if x'hx ≤ max