Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Williams, Kenneth S.
1969.
Small Solutions of the Congruence ax2 + by2 ≡ c(mod k).
Canadian Mathematical Bulletin,
Vol. 12,
Issue. 3,
p.
311.
Varbanets, P. D.
1970.
Lattice points in a circle whose distances from the center arein an arithmetic progression.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 8,
Issue. 6,
p.
917.
Williams, Kenneth S
1971.
A distribution property of the solutions of a congruence modulo a large prime.
Journal of Number Theory,
Vol. 3,
Issue. 1,
p.
19.
Callahan, T.
and
Smith, R. A.
1976.
𝐿-functions of a quadratic form.
Transactions of the American Mathematical Society,
Vol. 217,
Issue. 0,
p.
297.
Knopfmacher, J.
1981.
Initial Digits in Number Theory.
The Fibonacci Quarterly,
Vol. 19,
Issue. 2,
p.
121.
Nowak, Werner Georg
1985.
Zahlentheoretische Analysis.
Vol. 1114,
Issue. ,
p.
98.
Chalk, J.H.H.
1989.
Polynomial congruences over incomplete residue systems, modulo k.
Indagationes Mathematicae (Proceedings),
Vol. 92,
Issue. 1,
p.
49.
Duke, W.
Friedlander, J. B.
and
Iwaniec, H.
1994.
A quadratic divisor problem.
Inventiones Mathematicae,
Vol. 115,
Issue. 1,
p.
209.
Friedlander, John B.
and
Iwaniec, Henryk
2009.
Hyperbolic prime number theorem.
Acta Mathematica,
Vol. 202,
Issue. 1,
p.
1.
Blomer, V.
Brüdern, J.
and
Dietmann, R.
2009.
Sums of smooth squares.
Compositio Mathematica,
Vol. 145,
Issue. 6,
p.
1401.
Tolev, D. I.
2012.
On the remainder term in the circle problem in an arithmetic progression.
Proceedings of the Steklov Institute of Mathematics,
Vol. 276,
Issue. 1,
p.
261.
Fomenko, O. M.
2014.
Lattice Points in the Circle and Sphere.
Journal of Mathematical Sciences,
Vol. 200,
Issue. 5,
p.
632.
MANGEREL, ALEXANDER P.
2023.
Sign changes of fourier coefficients of holomorphic cusp forms at norm form arguments.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 175,
Issue. 3,
p.
539.
Kurlberg, Pär
Lester, Stephen
and
Rosenzweig, Lior
2023.
Superscars for arithmetic point scatters II.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,


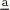 positive integer, we have had to obtain non-trivial estimates for the error term in the asymptotic expansion of
positive integer, we have had to obtain non-trivial estimates for the error term in the asymptotic expansion of