Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T09:23:24.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Characters on C(X)

Published online by Cambridge University Press:  20 November 2018

Karim Boulabiar
Karim Boulabiar*
Affiliation:
Research Laboratory of Algebra, Topology, Arithmetic, and Order, Faculty of Mathematical, Physical and Natural Sciences of Tunis, Tunis-El Manar University, 2092-El Manar, Tunisia. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The precise condition on a completely regular space 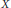$X$ for every character on 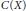$C\left( X \right)$ to be an evaluation at some point in 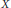$X$ is that 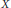$X$ be realcompact. Usually, this classical result is obtained by relying heavily on involved (and even nonconstructive) extension arguments. This note provides a direct proof that is accessible to a large audience.

Keywords

54C3046E25charactersrealcompactevaluationreal-valued continuous functions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 1 , 01 March 2015 , pp. 7 - 8
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Aron, R. M. and Fricke, G. H., Homomorphisms on C(R). Amer. Math. Monthly 93 (1986), 555. http://dx.doi.org/10.2307/2323033 Google Scholar
[2] Boulabiar, K., Real-valued ring homomorphisms on C Amer. Math. Monthly 121 (2014), 81–82. http://dx.doi.org/10.4169/amer.math.monthly.121.01.081 Google Scholar
[3] Ercan, Z. and Önal, S., A remark of the homomorphism on C(X) Proc. Amer. Math. Soc. 133 (2005), 3609–3611. http://dx.doi.org/10.1090/S0002-9939-05-07930-X Google Scholar
[4] Garrido, M. I., Gomez, J., and Jaramillo, J. A., Homomorphisms on function algebras. Canad. J. Math. 46 (1994), 734–745. http://dx.doi.org/10.4153/CJM-1994-041-3 Google Scholar
[5] Gillman, L. and Jerison, M., Rings of Continuous Functions. Springer-Verlag, New York, 1976.Google Scholar
[6] Ransford, T. J., Characters and point evaluations. Canad. Math. Bull. 38 (1995), 237–241. http://dx.doi.org/10.4153/CMB-1995-034-6 Google Scholar
[7] Shirota, T., A class of topological spaces. Osaka Math. J. 4 (1952), 23–40. Google Scholar