Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T01:11:57.829Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizing Two-Dimensional Maps Whose Jacobians Have Constant Eigenvalues

Published online by Cambridge University Press:  20 November 2018

Marc Chamberland
Marc Chamberland*
Affiliation:
Department of Mathematics and Computer Science Grinnell College, Grinnell, Iowa 50112 USA, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recent papers have shown that 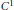${{C}^{1}}$ maps 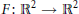$F:\,{{\mathbb{R}}^{2}}\,\to {{\mathbb{R}}^{2}}$ whose Jacobians have constant eigenvalues can be completely characterized if either the eigenvalues are equal or $F$ is a polynomial. Specifically, 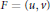$F\,=\,(u,\,v)$ must take the form

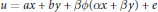$$u\,=\,ax\,+\,by\,+\,\beta \phi (\alpha x\,+\,\beta y)\,+\,e$$
$$v\,=\,cx\,+\,dy\,-\,\alpha \phi \,(\alpha x\,+\,\beta y)\,+\,f$$

for some constants $a,\,b,\,c,\,d,\,e,\,f,\,\alpha ,\,\beta $ and a 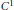${{C}^{1}}$ function 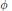$\phi $ in one variable. If, in addition, the function 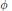$\phi $ is not affine, then

1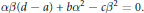

$$\alpha \beta (d\,-\,a)\,+\,b{{\alpha }^{2}}\,-\,c{{\beta }^{2}}\,=\,0.$$

This paper shows how these theorems cannot be extended by constructing a real-analytic map whose Jacobian eigenvalues are 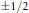$\pm 1/2$ and does not fit the previous form. This example is also used to construct non-obvious solutions to nonlinear PDEs, including the Monge—Ampère equation.

Keywords

26B1014R1535L70Jacobian ConjectureinjectivityMonge—Ampère equation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 3 , 01 September 2003 , pp. 323 - 331
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Campbell, L. A., Unipotent Jacobian Matrices and Univalent Maps. Combinatorial and computational algebra, Hong Kong, 1999, Contemp.Math. 264 (2000), 157–177.Google Scholar
[2] Chamberland, M., Diffeomorphic real-analytic maps and the Jacobian conjecture. Boundary value problems and related topics, Math. Comput.Modelling (5–6) 32 (2000), 727–732.Google Scholar
[3] Chamberland, M. and Meisters, G. H., A mountain pass to the Jacobian conjecture. Canad. Math. Bull. (4) 41 (1998), 442–451.Google Scholar
[4] Chen, Y. Q., A note on holomorphic maps with unipotent Jacobian matrices. Proc. Amer.Math. Soc. (7) 127 (1999), 2041–2044.Google Scholar
[5] Cima, A., Gasull, A. and Mañosas, F., The Discrete Markus-Yamabe Problem. Nonlinear Anal. 35 (1999), 343–354.Google Scholar
[6] Cobo, M., Gutierrez, C. and Llibre, J., On the Injectivity of C1 Maps of the Real Plane. Manuscript, (2001).Google Scholar
[7] Dillen, F., Polynomials with constant Hessian determinant. J. Pure Appl. Algebra (1) 71 (1991), 13–18.Google Scholar
[8] van den Essen, A., Polynomial Automorphisms and the Jacobian conjecture. Progress in Math. 190, Birkhuser Verlag, Basel, 2000.Google Scholar
[9] Garabedian, P. R., Partial Differential Equations. John Wiley & Sons, New York, 1964.Google Scholar
[10] Jörgens, K., Über die Lösungen der Differentialgleichung rt − s2 = 1. Math. Ann. 127 (1954), 130–134.Google Scholar
[11] Kusano, T. and Swanson, Charles A., Existence Theorems for Elliptic Monge.Ampère Equations in the Plane. Differential Integral Equations (3) 3 (1990), 487–493.Google Scholar
[12] Strang, G., Linear Algebra and its Applications, 3rd edition. Harcourt Brace Jovanovich, Inc., San Diego, 1988.Google Scholar
[13] Taylor, A. E. and Mann, W. R., Advanced Calculus, 2nd edition. John Wiley & Sons, New York, 1972.Google Scholar