Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T04:29:10.037Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizations of Three Classes of Zero-Divisor Graphs

Published online by Cambridge University Press:  20 November 2018

John D. LaGrange
John D. LaGrange*
Affiliation:
School of Natural Sciences, Indiana University Southeast, New Albany, Indiana 47150, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The zero-divisor graph $\Gamma (R)$ of a commutative ring $R$ is the graph whose vertices consist of the nonzero zero-divisors of $R$ such that distinct vertices $x$ and $y$ are adjacent if and only if 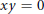$xy\,=\,0$. In this paper, a characterization is provided for zero-divisor graphs of Boolean rings. Also, commutative rings $R$ such that $\Gamma (R)$ is isomorphic to the zero-divisor graph of a direct product of integral domains are classified, as well as those whose zero-divisor graphs are central vertex complete.

Keywords

13A9913M99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 1 , 01 March 2012 , pp. 127 - 137
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Anderson, D. F., Levy, R., and Shapiro, J., Zero-divisor graphs, von Neumann regular rings, and Boolean algebras. J. Pure Appl. Algebra 180(2003), no. 3, 221–241. doi:10.1016/S0022-4049(02)00250-5Google Scholar
[2] Anderson, D. F. and Livingston, P. S., The zero-divisor graph of a commutative ring. J. Algebra 217(1999), no. 2, 434–447. doi:10.1006/jabr.1998.7840Google Scholar
[3] Beck, I., Coloring of commutative rings. J. Algebra 116(1988), no. 1, 208–226. doi:10.1016/0021-8693(88)90202-5Google Scholar
[4] DeMeyer, F. and Schneider, K., Automorphisms and zero-divisor graphs of commutative rings. In: Commutative Rings. Nova Sci. Publ., Hauppauge, NY, 2002, pp. 25–37.Google Scholar
[5] Fine, N. J., Gillman, L., and Lambek, J., Rings of Quotients of Rings of Functions. McGill University Press, Montreal, 1966.Google Scholar
[6] Kaplansky, I., Commutative Rings. Revised edition. University of Chicago Press, Chicago, 1974.Google Scholar
[7] LaGrange, J. D., Complemented zero-divisor graphs and Boolean rings. J. Algebra 315(2007), no. 2, 600–611. doi:10.1016/j.jalgebra.2006.12.030Google Scholar
[8] LaGrange, J. D., The cardinality of an annihilator class in a von Neumann regular ring. Int. Electron. J. Algebra 4(2008), 63–82.Google Scholar
[9] LaGrange, J. D., On realizing zero-divisor graphs. Comm. Algebra 36(2008), no. 12, 4509–4520. doi:10.1080/00927870802182499Google Scholar
[10] Lam, T. Y., Lectures on Modules and Rings. Graduate Texts in Mathematics 189. Springer-Verlag, New York, 1998.Google Scholar
[11] Lambek, J., Lectures on Rings and Modules. Blaisdell Publishing Company, Waltham, MA, 1966.Google Scholar
[12] Lu, D. and Wu, T., The zero-divisor graphs which are uniquely determined by neighborhoods. Comm. Algebra 35(2007), no. 12, 3855–3864. doi:10.1080/00927870701509156Google Scholar
[13] Redmond, S. P., On zero-divisor graphs of small finite commutative rings. Discrete Math. 307(2007), no. 9-11, 1155–1166. doi:10.1016/j.disc.2006.07.025Google Scholar
[14] Sikorski, R., Boolean Algebras. Third edition. Ergebnisse derMathematik und ihrer Grenzgebiete 25. Springer-Verlag, New York, 1969.Google Scholar