Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T19:00:55.042Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of singular Schrödinger operators on the half-line

Part of: Nonstandard models Asymptotic theory Ordinary differential operators Other (nonclassical) types of operator theory Real functions: Miscellaneous topics Elliptic equations and systems

Published online by Cambridge University Press:  07 December 2020

Raffaele Scandone ,
Lorenzo Luperi Baglini  and
Kyrylo Simonov
Raffaele Scandone*
Affiliation:
Gran Sasso Science Institute, Viale F. Crispi 7, 67100 L'Aquila, Italy
Lorenzo Luperi Baglini
Affiliation:
Dipartimento di Matematica, Università di Milano, Via Saldini 50, 20133Milano, Italy e-mail: [email protected]
Kyrylo Simonov
Affiliation:
Fakultät für Mathematik, Universität Wien, Oskar-Morgenstern-Platz 1, 1090Vienna, Austria e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a class of delta-like perturbations of the Laplacian on the half-line, characterized by Robin boundary conditions at the origin. Using the formalism of nonstandard analysis, we derive a simple connection with a suitable family of Schrödinger operators with potentials of very large (infinite) magnitude and very short (infinitesimal) range. As a consequence, we also derive a similar result for point interactions in the Euclidean space 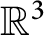$\mathbb {R}^3$ , in the case of radial potentials. Moreover, we discuss explicitly our results in the case of potentials that are linear in a neighborhood of the origin.

Keywords

Schrödinger operatorssingular perturbationspoint interactionsnonstandard analysis

MSC classification

Primary: 34L40: Particular operators (Dirac, one-dimensional Schrödinger, etc.) 34E15: Singular perturbations, general theory 35J10: Schrödinger operator 03H05: Nonstandard models in mathematics 26E35: Nonstandard analysis
Secondary: 47S20: Nonstandard operator theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 923 - 941
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of L.L.B. was supported by grant P 30821-N35 of the Austrian Science Fund FWF, and the research of K.S was supported by grant P 30821-N35 of the Austrian Science Fund FWF.

References

Albeverio, S., Brzeźniak, Z., and Da̧browski, L., Fundamental solution of the heat and Schrödinger equations with point interaction . J. Funct. Anal. 130(1995), 220–254.CrossRefGoogle Scholar
Albeverio, S., Fenstad, J. E., and Høegh-Krohn, R., Singular perturbations and nonstandard analysis . Trans. Amer. Math. Soc. 252(1979), 275–295.CrossRefGoogle Scholar
Albeverio, S. and Figari, R., Quantum fields and point interactions . Rend. Mat. Appl. 39(2018), 161–180.Google Scholar
Albeverio, S., Gesztesy, F., Høegh-Krohn, R., and Holden, H., Solvable models in quantum mechanics . Texts and Monographs in Physics, Springer, New York, 1988.CrossRefGoogle Scholar
Albeverio, S. and Høegh-Krohn, R., Point interactions as limits of short range interactions . J. Oper. Theory 6(1981), 313–339.Google Scholar
Albeverio, S. and Kurasov, P., Singular perturbations of differential operators: solvable Schrödinger-type operators . London Mathematical Society Lecture Note Series, 271, Cambridge University Press, Cambridge, 2000.CrossRefGoogle Scholar
Benci, V., Di Nasso, M., and Forti, M., The eightfold path to nonstandard analysis . In: Cutland, N. J., Di Nasso, M., and Ross, D. A. (eds.), Nonstandard methods and applications in mathematics, Lecture Notes in Logic, 25, ASL and A. K. Peters, Wellesley, 2006, pp. 3–44.Google Scholar
Benci, V., Luperi Baglini, L., and Simonov, K., Infinitesimal and infinite numbers as an approach to quantum mechanics . Quantum 3(2019), 137, 22 pp.CrossRefGoogle Scholar
Berezin, F. A. and Faddeev, L. D., A remark on Schrödinger's equation with a singular potential . Sov. Math. Dokl. 2(1961), 372–375.Google Scholar
Bethe, H. and Peierls, R., Quantum theory of the diplon . Proc. Royal Soc. A. 148(1935), 146–156.Google Scholar
Bethe, H. A. and Peierls, R., The scattering of neutrons by protons . Proc. Roy. Soc. A. 149(1935), 176–183.Google Scholar
Chang, C. C. and Keisler, H. J., Model theory . 3rd ed., North-Holland, Amsterdam, Netherlands, 1990.Google Scholar
Dell'Antonio, G., Figari, R., and Teta, A., A brief review on point interactions . In: Bonilla, L. L. (ed.), Inverse problems and imaging: lectures given at the C.I.M.E. Summer School held in Martina Franca, Italy, September 15–21, 2002, Lecture Notes in Mathematics, 1943, Springer, Berlin, 2008, pp. 171–189.CrossRefGoogle Scholar
Dell'Antonio, G. and Michelangeli, A., Schrödinger operators on half-line with shrinking potentials at the origin . Asymptot. Anal. 97(2016), 113–138.CrossRefGoogle Scholar
Dell'Antonio, G., Michelangeli, A., Scandone, R., and Yajima, K., ${L}^p$ -boundedness of wave operators for the three-dimensional multi-centre point interaction . Ann. Henri Poincaré. 19(2018), 283–322.CrossRefGoogle Scholar
Dugandžija, N. and Nedeljkov, M., Generalized solution to multidimensional cubic Schrödinger equation with delta potential . Monatsh. Math. 190(2019), 481–499.CrossRefGoogle Scholar
Gitman, D. M., Tyutin, I. V., and Voronov, B. L., Self-adjoint extensions in quantum mechanics: general theory and applications to Schrödinger and Dirac equations with singular potentials . Progress in Mathematical Physics, 62, Birkäuser/Springer, New York, NY, 2012.CrossRefGoogle Scholar
Goldblatt, R., Lectures on the hyperreals: an introduction to nonstandard analysis . Graduate Texts in Mathematics, 188, Springer, Berlin, 1998.CrossRefGoogle Scholar
Golovaty, Y. D. and Hryniv, R. O., On norm resolvent convergence of Schrödinger operators with ${\delta}^{\prime }$ -like potentials . J. Phys. A 43(2010), 155204, 14.CrossRefGoogle Scholar
Golovaty, Y. D. and Hryniv, R. O., Norm resolvent convergence of singularly scaled Schrödinger operators and ${\delta}^{\prime }$ -potentials . Proc. Roy. Soc. Edinb. A 143(2013), 791–816.CrossRefGoogle Scholar
Grossmann, A., Høegh-Krohn, R., and Mebkhout, M., A class of explicitly soluble, local, many-center Hamiltonians for one-particle quantum mechanics in two and three dimensions. I . J. Math. Phys. 21(1980), 2376–2385.CrossRefGoogle Scholar
Grossmann, A., Høegh-Krohn, R., and Mebkhout, M., The one particle theory of periodic point interactions: polymers, monomolecular layers, and crystals . Comm. Math. Phys. 77(1980), 87–110.CrossRefGoogle Scholar
Hörmann, G., The Cauchy problem for Schrödinger-type partial differential operators with generalized functions in the principal part and as data . Monatsh. Math. 163(2011), 445–460.CrossRefGoogle Scholar
Kronig, R. de L. and Penney, W. G., Quantum mechanics of electrons in crystal lattices . Proc. Roy. Soc. A. 130(1931), 499–513.Google Scholar
Michelangeli, A. and Ottolini, A., On point interactions realised as Ter-Martirosyan–Skornyakov Hamiltonians . Rep. Math. Phys. 79(2017), 215–260.CrossRefGoogle Scholar
Michelangeli, A., Ottolini, A., and Scandone, R., Fractional powers and singular perturbations of quantum differential Hamiltonians . J. Math. Phys. 59(2018), 072106, 27.CrossRefGoogle Scholar
Michelangeli, A. and Scandone, R., Point-like perturbed fractional Laplacians through shrinking potentials of finite range . Complex Anal. Oper. Theory 13(2019), 3717–3752.CrossRefGoogle Scholar
Nelson, E., Internal set theory: a new approach to nonstandard analysis . Bull. Amer. Math. Soc. 83(1977), 1165–1198.CrossRefGoogle Scholar
Olver, F. W. J., Asymptotics and special functions . A. K. Peters, Wellesley, 1997. Reprint of the 1974 original.CrossRefGoogle Scholar
Posilicano, A., A Krein-like formula for singular perturbations of self-adjoint operators and applications . J. Funct. Anal. 183(2001), 109–147.CrossRefGoogle Scholar
Reed, M. and Simon, B., Methods of modern mathematical physics. II: Fourier analysis, self-adjointness . Academic Press, New York, NY, 1975.Google Scholar
Scarlatti, S. and Teta, A., Derivation of the time-dependent propagator for the three-dimensional Schrödinger equation with one-point interaction . J. Phys. A 23(1990), L1033–L1035.CrossRefGoogle Scholar
Schmüdgen, K., Unbounded self-adjoint operators on Hilbert space . Graduate Texts in Mathematics, 265, Springer, Dordrecht, Netherlands, 2012.CrossRefGoogle Scholar
Šeba, P., Schrödinger particles on a half line . Lett. Math. Phys. 10(1985), 21–27.CrossRefGoogle Scholar
Sickel, W., Yang, D., and Yuan, W., The radial lemma of Strauss in the context of Morrey spaces . Ann. Acad. Sci. Fenn. Math. 39(2014), 417–442.CrossRefGoogle Scholar
Thomas, L. H., The interaction between a neutron and a proton and the structure of ${H}^3$ . Phys. Rev. 47(1935), 903–909.CrossRefGoogle Scholar