Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Strichartz, Robert S.
1993.
Characterization of eigenfunctions of the Laplacian by boundedness conditions.
Transactions of the American Mathematical Society,
Vol. 338,
Issue. 2,
p.
971.
Kumar, Pratyoosh
Ray, Swagato
and
Sarkar, Rudra
2013.
Characterization of almost 𝐿^{𝑝}-eigenfunctions of the Laplace-Beltrami operator.
Transactions of the American Mathematical Society,
Vol. 366,
Issue. 6,
p.
3191.
Ray, Swagato K.
and
Sarkar, Rudra P.
2014.
A Theorem of Roe and Strichartz for Riemannian Symmetric Spaces of Noncompact Type.
International Mathematics Research Notices,
Vol. 2014,
Issue. 5,
p.
1273.
Mejjaoli, Hatem
and
Trimèche, Khalifa
2014.
Characterization of the support for the hypergeometric Fourier transform of the W-invariant functions and distributions on
R
d
and Roe’s theorem.
Journal of Inequalities and Applications,
Vol. 2014,
Issue. 1,
Andersen, Nils Byrial
2015.
Roe's theorem revisited.
Integral Transforms and Special Functions,
Vol. 26,
Issue. 3,
p.
165.
Andersen, Nils Byrial
2015.
Real Paley–Wiener theorems and Roe's theorem associated with the Opdam–Cherednik transform.
Journal of Mathematical Analysis and Applications,
Vol. 427,
Issue. 1,
p.
47.
Mejjaoli, Hatem
2016.
Spectral theorems associated with the Cherednik operators on $$\mathbb {R}^{d}$$ R d.
Afrika Matematika,
Vol. 27,
Issue. 5-6,
p.
1091.
Mejjaoli, Hatem
2016.
SPECTRAL THEOREMS ASSOCIATED TO THE DUNKL OPERATORS.
Korean Journal of Mathematics,
Vol. 24,
Issue. 4,
p.
693.
Mejjaoli, Hatem
2016.
Paley–Wiener Theorems of Generalized Fourier Transform Associated with a Cherednik Type Operator on the Real Line.
Complex Analysis and Operator Theory,
Vol. 10,
Issue. 6,
p.
1145.
Mejjaoli, Hatem
2016.
On the range of the Opdam–Cherednik transform and Roe’s theorem in the Cherednik setting.
Journal of Pseudo-Differential Operators and Applications,
Vol. 7,
Issue. 1,
p.
19.
Mejjaoli, Hatem
2017.
Paley-Wiener Theorems for the Two-Sided Quaternion Fourier Transform.
Advances in Applied Clifford Algebras,
Vol. 27,
Issue. 2,
p.
1611.
Naik, Muna
and
Sarkar, Rudra P.
2020.
Characterization of eigenfunctions of the Laplace–Beltrami operator using Fourier multipliers.
Journal of Functional Analysis,
Vol. 279,
Issue. 11,
p.
108737.
Rano, Sumit Kumar
2022.
A theorem of Roe and Strichartz on homogeneous trees.
Forum Mathematicum,
Vol. 34,
Issue. 1,
p.
115.
Bagchi, Sayan
Kumar, Ashisha
and
Sen, Suparna
2023.
Roe–Strichartz theorem on two‐step nilpotent Lie groupsa.
Mathematische Nachrichten,
Vol. 296,
Issue. 7,
p.
2691.
Rano, Sumit Kumar
and
Sarkar, Rudra P.
2025.
A theorem of Strichartz for multipliers on homogeneous trees.
Mathematische Zeitschrift,
Vol. 309,
Issue. 1,
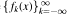 is a sequence of functions on ℝn with Δfk = fk+1 (where Δ is the Laplacian) that satisfies the growth condition: |fk(x)| ≤ Mk{1 + |x|)a where a ≥ 0 and the constants have sublinear growth
is a sequence of functions on ℝn with Δfk = fk+1 (where Δ is the Laplacian) that satisfies the growth condition: |fk(x)| ≤ Mk{1 + |x|)a where a ≥ 0 and the constants have sublinear growth 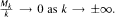 Then Δf0 = —f0- This characterizes eigenfunctions f of Δ with polynomial growth in terms of the size of the powers Δkf, —∞ < k < ∞. It also generalizes results of Roe (where a = 0, Mk = M, and n = 1 ) and Strichartz (where a = 0, Mk = M for n). The analogue holds for formally self-adjoint constant coefficient linear partial differential operators on ℝn.
Then Δf0 = —f0- This characterizes eigenfunctions f of Δ with polynomial growth in terms of the size of the powers Δkf, —∞ < k < ∞. It also generalizes results of Roe (where a = 0, Mk = M, and n = 1 ) and Strichartz (where a = 0, Mk = M for n). The analogue holds for formally self-adjoint constant coefficient linear partial differential operators on ℝn.