Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-21T10:58:58.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Characteristic Varieties for a Class of Line Arrangements

Published online by Cambridge University Press:  20 November 2018

Thi Anh Thu Dinh
Thi Anh Thu Dinh*
Affiliation:
Laboratoire J. A. Dieudonné, Université de Nice Sophia Antipolis, Parc Valrose, 06108 Nice Cedex 02, Francee-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 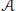$\mathcal{A}$ be a line arrangement in the complex projective plane ${{\mathbb{P}}^{2}}$, having the points of multiplicity 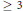$\ge \,3$ situated on two lines in 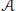$\mathcal{A}$, say 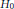${{H}_{0}}$ and 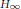${{H}_{\infty }}$. Then we show that the non-local irreducible components of the first resonance variety 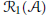${{\mathcal{R}}_{1}}(\mathcal{A})$ are 2-dimensional and correspond to parallelograms 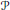$P$ in 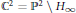${{\mathbb{C}}^{2}}={{\mathbb{P}}^{2}}\text{ }\backslash \text{ }{{H}_{\infty }}$ whose sides are in 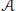$\mathcal{A}$ and for which 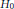${{H}_{0}}$ is a diagonal.

Keywords

14C2114F9932S2214E0514H50local systemline arrangementcharacteristic varietyresonance variety
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 1 , 01 March 2011 , pp. 56 - 67
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Choudary, A. D. R., Dimca, A., and Papadima, S., Some analogs of Zariski's Theorem on nodal line arrangements. Algebr. Geom. Topol. 5(2005), 691–711. doi:10.2140/agt.2005.5.691Google Scholar
[2] Cohen, D. C. and Suciu, A. I., Characteristic varieties of arrangements. Math. Proc. Cambridge Philos. Soc. 127(1999), no. 1, 33–53. doi:10.1017/S0305004199003576Google Scholar
[3] Dimca, A., Sheaves in topology. Universitext, Springer-Verlag, Berlin, 2004.Google Scholar
[4] Dimca, A., Pencils of plane curves and characteristic varieties. http://arxiv.org/abs/math/0606442.Google Scholar
[5] Dimca, A., On admissible rank one local systems. J. Algebra 321(2009), no. 11, 3145–3157. doi:10.1016/j.jalgebra.2008.01.039Google Scholar
[6] Dimca, A., Papadima, S., and Suciu, A., Formality, Alexander invariants, and a question of Serre. http://arxiv.org/abs/math/0512480.Google Scholar
[7] Dimca, A. and Maxim, L., Multivariable Alexander invariants of hypersurface complements. Trans. Amer. Math. Soc. 359(2007), no. 7, 3505–3528. doi:10.1090/S0002-9947-07-04241-9Google Scholar
[8] Esnault, H., Schechtman, V., and Viehweg, E., Cohomology of local systems on the complement of hyperplanes. Invent. Math. 109(1992), no. 3, 557–561; Erratum, ibid. 112(1993), 447. doi:10.1007/BF01232040Google Scholar
[9] Falk, M., Arrangements and cohomology. Ann. Combin. 1(1997), no. 2, 135–157. doi:10.1007/BF02558471Google Scholar
[10] Libgober, A. and Yuzvinsky, S., Cohomology of the Orlik-Solomon algebras and local systems. Compositio Math. 121(2000), no. 3, 337–361. doi:10.1023/A:1001826010964Google Scholar
[11] Orlik, P. and Terao, H., Arrangements of hyperplanes. Grundlehren der Mathematischen Wissenschaften, 300, Springer Verlag, Berlin, 1992.Google Scholar
[12] Nazir, S. and Raza, Z., Admissible local systems for a class of line arrangements. Proc. Amer. Math. Soc. 137(2009), no. 4, 1307–1313. doi:10.1090/S0002-9939-08-09661-5Google Scholar
[13] Papadima, S. and Suciu, A., Algebraic invariants for right-angled Artin groups. Math. Ann. 334(2006), no. 3, 533–555. doi:10.1007/s00208-005-0704-9Google Scholar
[14] Papadima, S. and Suciu, A., Toric complexes and Artin kernels. Adv. Math. 220(2009), no. 2, 441–477. doi:10.1016/j.aim.2008.09.008Google Scholar
[15] Schechtman, V., Terao, H., and Varchenko, A., Local systems over complements of hyperplanes and the Kac-Kazhdan conditions for singular vectors. J. Pure Appl. Alg. 100(1995), no. 1–3, 93–102. doi:10.1016/0022-4049(95)00014-NGoogle Scholar
[16] Suciu, A., Translated tori in the characteristic varieties of complex hyperplane arrangements. Arrangements in Boston: a Conference on Hyperplane Arrangements (1999). Topology Appl. 118(2002), no. 1–2, 209–223. doi:10.1016/S0166-8641(01)00052-9Google Scholar