Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T14:13:02.371Z Has data issue: false hasContentIssue false
  • English
  • Français

Character Sums with Division Polynomials

Published online by Cambridge University Press:  20 November 2018

Igor E. Shparlinski  and
Katherine E. Stange
Igor E. Shparlinski
Affiliation:
Department of Computing, Macquarie University, North Ryde, Sydney, NSW 2109, Australiae-mail: [email protected]
Katherine E. Stange
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, USAe-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain nontrivial estimates of quadratic character sums of division polynomials 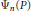${{\text{ }\!\!\psi\!\!\text{ }}_{n}}\left( P \right)$, 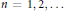$n\,=\,1,\,2,\,\ldots $ , evaluated at a given point $P$ on an elliptic curve over a finite field of $q$ elements. Our bounds are nontrivial if the order of $P$ is at least 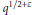${{q}^{{}^{1}/{}_{2+\varepsilon }}}$ for some fixed 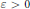$\varepsilon \,>\,0$. This work is motivated by an open question about statistical indistinguishability of some cryptographically relevant sequences that was recently brought up by K. Lauter and the second author.

Keywords

11L4014H52division polynomial, character sum
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 4 , 01 December 2012 , pp. 850 - 857
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Chen, Z., Elliptic curve analogue of Legendre sequences. Monatsh. Math. 154(2008), no. 1, 1–10. http://dx.doi.org/10.1007/s00605-008-0520-x Google Scholar
[2] Everest, G., van der Poorten, A. J., Shparlinski, I. E., and Ward, T., Recurrence Sequences. Mathematical Surveys and Monographs 104. American Mathematical Society, Providence, RI, 2003.Google Scholar
[3] Iwaniec, H. and Kowalski, E., Analytic Number Theory. American Mathematical Society Colloquium Publications 53. American Mathematical Society, Providence, RI, 2004.Google Scholar
[4] Kohel, D. R. and Shparlinski, I. E., On exponential sums and group generators for elliptic curves over finite fields. Lecture Notes in Comput. Sci. 1838, Springer, Berlin, 2000, pp. 395–404.Google Scholar
[5] Lauter, K. E. and Stange, K. E., The elliptic curve discrete logarithm problem and equivalent hard problems for elliptic divisibility sequences. Lecture Notes in Comput. Sci. 5381, Springer-Verlag, Berlin, 2009, pp. 309–327.Google Scholar
[6] Perret, M., Multiplicative character sums and Kummer coverings. Acta Arith. 59(1991), no. 3, 279–290.Google Scholar
[7] Russell, A. C. and Shparlinski, I. E., Classical and quantum function reconstruction via character evaluation. J. Complexity 20(2004), no. 2-3, 404–422. http://dx.doi.org/10.1016/j.jco.2003.08.019 Google Scholar
[8] Shparlinski, I. E., Distribution of nonresidues and primitive roots in recurrent sequences. Mat. Zametki 24(1978), no. 5, 603–613, 733, (in Russian).Google Scholar
[9] Silverman, J. H., The Arithmetic of Elliptic Curves. Second edition. Graduate Texts in Mathematics 106. Springer, Dordrecht, 2009.Google Scholar
[10] Silverman, J. H., p-adic properties of division polynomials and elliptic divisibility sequences. Math. Ann. 332(2005), no. 2, 443–471. http://dx.doi.org/10.1007/s00208-004-0608-0 Google Scholar
[11] Swart, C., Elliptic Curves and Related Sequences. Ph.D. thesis, Royal Holloway and Bedford New College, University of London, 2003.Google Scholar
[12] Ward, M., Memoir on elliptic divisibility sequences. Amer. J. Math. 70(1948), 31–74. http://dx.doi.org/10.2307/2371930 Google Scholar