Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-08T14:25:16.179Z Has data issue: false hasContentIssue false
  • English
  • Français

Character Density in Central Subalgebras of Compact Quantum Groups

Published online by Cambridge University Press:  20 November 2018

Mahmood Alaghmandan  and
Jason Crann
Mahmood Alaghmandan
Affiliation:
Department of Mathematical Sciences, Chalmers University of Technology and University of Gothenburg, Gothenburg SE-412 96, Sweden. e-mail: [email protected]
Jason Crann
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON, KIS 5B6. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate quantum group generalizations of various density results from Fourier analysis on compact groups. In particular, we establish the density of characters in the space of fixed points of the conjugation action on 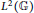${{L}^{2}}(\mathbb{G})$ and use this result to show the 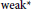$\text{wea}{{\text{k}}^{\star }}$ density and normal density of characters in 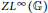$Z{{L}^{\infty }}(\mathbb{G})$ and 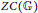$ZC(\mathbb{G})$, respectively. As a corollary, we partially answer an open question of Woronowicz. At the level of 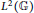${{L}^{1}}(\mathbb{G})$, we show that the center 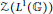$~z({{L}^{1}}(\mathbb{G}))$ is precisely the closed linear span of the quantum characters for a large class of compact quantum groups, including arbitrary compact Kac algebras. In the latter setting, we show, in addition, that 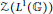$~z({{L}^{1}}(\mathbb{G}))$ is a completely complemented 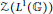$~z({{L}^{1}}(\mathbb{G}))$-submodule of 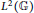${{L}^{2}}(\mathbb{G})$.

Keywords

43A2043A4046J40compact quantum groupirreducible character
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 3 , 01 September 2017 , pp. 449 - 461
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Arano, Y., Unitary spherical representations ofDrinfeld doubles. J. Reine Angew. Math., to appear. http://dx.doi.Org/10.1515/crelle-2O15-0079 Google Scholar
[2] Banica, T., Theorie des representations du groupe quantique compact libre O(n). C. R. Acad. Sci. Paris Ser. I Math. 322(1996), no. 3, 241–244. Google Scholar
[3] Bedos, E. and Tuset, L., Amenability and co-amenability for locally compact quantum groups. Internat. J. Math. 14(2003), no. 8, 865–884. http://dx.doi.Org/10.11 42/S01291 67X03002046 Google Scholar
[4] Brannan, M., Approximation properties for free orthogonal and free unitary quantum groups. J. Reine Angew. Math. 672(2012), 223–251. Google Scholar
[5] De Commer, K., Freslon, A., and Yamashita, M., CCAPfor universal discrete quantum groups. Comm. Math. Phys. 331(2014), no. 2, 677–701. http://dx.doi.Org/10.1007/s00220-014-2052-7 Google Scholar
[6] Daws, M., Operator biprojectivity of compact quantum groups. Proc. Amer. Math. Soc. 138(2010), no. 4, 1349–1359. http://dx.doi.Org/10.1090/S0002-9939-09-10220-4 Google Scholar
[7] Enock, M. and Schwartz, J. M., Kac algebras and duality of locally compact groups. Springer-Verlag, Berlin, 1992. http://dx.doi.Org/10.1007/978-3-662-02813-1 Google Scholar
[8] Kustermans, J., Locally compact quantum groups in the universal setting. Internat. J. Math. 12(2001), no. 3, 289–338. http://dx.doi.Org/1 0.1142/S012 91 67X01000757 Google Scholar
[9] Kustermans, J. and Vaes, S., Locally compact quantum groups. Ann. Sci. Ecole Norm. Sup. (4) 33(2000), no. 6, 837–934. http://dx.doi.Org/10.1016/S0012-9593(00)01055-7 Google Scholar
[10] Kustermans, J. and Vaes, S., Locally compact quantum groups in the von Neumann algebraic setting. Math. Scand. 92(2003), no. 1, 68–92. http://dx.doi.Org/10.7146/math.scand.a-14394 Google Scholar
[11] Lemeux, E., Haagerup approximation property for quantum reflection groups. Proc. Amer. Math. Soc. 143(2015), no. 5, 2017–2031. http://dx.doi.Org/10.1090/S0002-9939-2015-12402-1 Google Scholar
[12] Mosak, R. D., The Ll- and C*-algebras o/[F7A]groups, and their representations. Trans. Amer. Math. Soc. 163(1972), 277–310. http://dx.doi.Org/10.2307/1995723 Google Scholar
[13] Neshveyev, S. and Tuset, L., Compact Quantum Groups and Their Representation Categories. Cours Specialises-Collection SMF, 20, Societe Mathematique de France, Paris, 2013. Google Scholar
[14] Ruan, Z.-J. and Xu, G., Splitting properties of operator bimodules and operator amenability ofKac algebras. In: Operator theory, operator algebras and related topics (Timisoara, 1996), Theta Found., Bucharest, 1997, pp. 193–216.Google Scholar
[15] Vaes, S., Locally compact quantum groups. Ph. D. thesis, K.U. Leuven, 2000.Google Scholar
[16] Woronowicz, S. L., Compact matrix pseudogroups. Comm. Math. Phys. 111(1987), no. 4, 613–665.Google Scholar