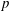Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-09T07:52:28.555Z Has data issue: false hasContentIssue false
  • English
  • Français

Character Codegrees of Maximal Class $p$-groups

Part of: Representation theory of groups

Published online by Cambridge University Press:  25 September 2019

Sarah Croome  and
Mark L. Lewis
Sarah Croome
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH 44242, United States Email: [email protected]@math.kent.edu
Mark L. Lewis
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH 44242, United States Email: [email protected]@math.kent.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 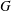$G$ be a 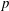$p$-group and let 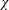$\unicode[STIX]{x1D712}$ be an irreducible character of 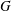$G$. The codegree of 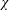$\unicode[STIX]{x1D712}$ is given by 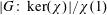$|G:\,\text{ker}(\unicode[STIX]{x1D712})|/\unicode[STIX]{x1D712}(1)$. If 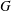$G$ is a maximal class 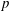$p$-group that is normally monomial or has at most three character degrees, then the codegrees of 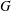$G$ are consecutive powers of 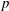$p$. If 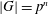$|G|=p^{n}$ and 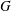$G$ has consecutive 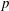$p$-power codegrees up to 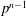$p^{n-1}$, then the nilpotence class of 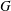$G$ is at most 2 or 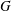$G$ has maximal class.

Keywords

codegreep-groupmaximal class

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20D15: Nilpotent groups, $p$-groups
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 2 , June 2020 , pp. 328 - 334
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berkovich, Y., Groups of prime power order. Vol. 1. De Gruyter Expositions in Mathematics, 46, De Gruyter, Berlin, 2008. https://doi.org/10.1515/9783110208238.512Google Scholar
Bosma, W., Cannon, J., and Playoust, C., The magma algebra system I: The user language. J. Symbolic Comput. 24(1997), 235–265. https://doi.org/10.1006/jsco.1996.0125Google Scholar
Du, N. and Lewis, M. L., Codegrees and nilpotence class of p-groups. J. Group Theory 19(2016), 561–567. https://doi.org/10.1515/jgth-2015-0039Google Scholar
Isaacs, I. M., Character theory of finite groups. AMS Chelsea Publishing, Providence, RI, 2006. https://doi.org/10.1090/chel/359Google Scholar
Mann, A., Character degrees of some p-groups. 2016. arxiv:1602.04689Google Scholar
Qian, G., Wang, Y., and Wei, H., Co-degrees of irreducible characters in finite groups. J. Algebra 312(2007), 946–955. https://doi.org/10.1016/j.jalgebra.2006.11.001Google Scholar
Slattery, M. C., Maximal class p-groups with large character degree gaps. Arch. Math. (Basel) 105(2015), 501–507. https://doi.org/10.1007/s00013-015-0836-4Google Scholar
Slattery, M. C., Character degrees of normally monomial maximal class 5-groups. Character theory of finite groups. Contemp. Math., 524, American Mathematical Society, Providence, RI, 2010, pp. 153–159. https://doi.org/10.1090/conm/524/10354Google Scholar