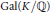Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Banks, William D.
and
Freiberg, Tristan
2016.
Carmichael numbers and the sieve.
Journal of Number Theory,
Vol. 165,
Issue. ,
p.
15.
Malik, Amita
and
Prabhu, Neha
2022.
Equidistribution of αpθ$\alpha p^{\theta }$ with a Chebotarev condition and applications to extremal primes.
Mathematika,
Vol. 68,
Issue. 3,
p.
595.