Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T07:07:38.170Z Has data issue: false hasContentIssue false
  • English
  • Français

The Carleson Measure Problem Between Analytic Morrey Spaces

Published online by Cambridge University Press:  20 November 2018

Jianfei Wang
Jianfei Wang*
Affiliation:
Mathematics, Physics and Information Engineering, ZhejiangNormalUniversity, Jinhua, Zhejiang, 321004, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to characterize positive measure $\mu$ on the unit disk such that the analytic Morrey space 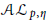$\mathcal{A}{{\mathcal{L}}_{p,\eta }}$ is boundedly and compactly embedded to the tent space

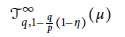$$\mathcal{J}_{q,1-\frac{q}{p}\left( 1-\eta \right)}^{\infty }\left( \mu \right)$$

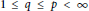for the case $1\,\le \,q\,\le \,p\,<\,\infty$ respectively. As an application, these results are used to establish the boundedness and compactness of integral operators and multipliers between analytic Morrey spaces.

Keywords

30H3528A1247B3846E15Morrey spaceCarleson measure problemboundednesscompactness
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 4 , 01 December 2016 , pp. 878 - 890
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Aleman, A. and Cima, J. A., An integral operator on HP and Hardy's inequality. J. Anal. Math. 85(2001), 157–176. http://dx.doi.Org/10.1007/BF02788078 Google Scholar
[2] Carleson, L., Interpolations by bounded analytic functions and the corona problem. Ann. of Math. 76(1962), 547–559. http://dx.doi.Org/10.2307/1970375 Google Scholar
[3] Cascante, C., Fabrega, J., and Ortega, J. M., The corona theorem in weighted Hardy and Morrey spaces. Ann. Scuola. Norm. Super. Pisa. Cl. Sci. 13(2014), no. 3, 579–607.Google Scholar
[4] Fefferman, C. and Stein, E. M., Hp spaces of several variables. Acta. Math. 129(1972), no. 3-4, 137–193. http://dx.doi.Org/10.1007/BF02392215 Google Scholar
[5] Kufner, A., O. John and Fcik, S., Function spaces. Monographs and textbooks on mechanics of solids and fluids; mechanics: analysis. Noordhoff International Publishing, Leyden, 1977.Google Scholar
[6] Li, P., Liu, J., and Lou, Z., Integral operators on analytic Morrey spaces. Sci China Math. 57(2014), no. 9, 1961–1974. http://dx.doi.Org/1 0.1007/s11425-014-4811 -5 Google Scholar
[7] Liu, J. and Lou, Z., Carleson measure for analytic Morrey spaces. Nonlinear Anal. 125(2015), 423–432. http://dx.doi.Org/10.1016/j.na.2O15.05.016 Google Scholar
[8] Morrey, C. B., On the solutions of quasi-linear elliptic partial differential equations. Trans. Amer. Math. Soc. 43(1938), no. 1, 126–166. http://dx.doi.Org/10.1090/S0002-9947-1938-1501936-8 Google Scholar
[9] Pommerenke, C., Schlichte Funktionen und analytische Funktionen von beschrankter mittlerer Oszillation. Comment. Math. Helv. 52(1978), no. 4, 591–602. http://dx.doi.Org/10.1007/BF02567392 Google Scholar
[10] Siskakis, A. G., Composition semigroups and the Cesáro operator on 3C. J. London Math. Soc. 36(1987), no. 1, 153–164. http://dx.doi.Org/10.1112/jlms/s2-36.1.153 Google Scholar
[11] Tjani, M., Compact composition operators on Besove spaces. Trans. Amer. Math. Soc. 355(2003), no. 11, 4683–4698. http://dx.doi.Org/10.1090/S0002-9947-03-03354-3 Google Scholar
[12] Wang, J. and J. Xiao , Analytic Campanato spaces by functionals and operators. J. Geom. Anal. http://dx.doi.Org/10.1007/s1222O-O15-9658-7 Google Scholar
[13] Wu, Z., A new characterization for Carleson measures and some applications. Integral Equations Operator Theory 71(2011), no. 2,161-180. http://dx.doi.Org/10.1007/s00020-011-1892-1 Google Scholar
[14] Wu, Z. and Xie, C., Q spaces and Morrey spaces. J. Funct. Anal. 201(2003), no. 1, 282–297. http://dx.doi.Org/10.101 6/SOO22-1236(03)00020-X Google Scholar
[15] Xiao, J., Geometric Qp functions. Frontiers in Mathematics, Birkhauser-Verlag, Basel, 2006.Google Scholar
[16] Xiao, J., The Qp Carleson measure problem. Adv. Math. 217(2008), no. 5, 2075–2088. http://dx.doi.Org/10.1016/j.aim.2007.08.015 Google Scholar
[17] Xiao, J. and W Xu, Composition operators between analytic Campanato space. J. Geom. Anal. 24(2014), no. 2, 649–666. http://dx.doi.Org/10.1007/s12220-012-9349-6 Google Scholar
[18] Xiao, J. and Yuan, C., Analytic Campanato spaces and their compositions. Indiana. Univ. Math. J. 64(2015), no. 4, 1001–1025. http://dx.doi.Org/10.1512/iumj.2015.64.5575 Google Scholar
[19] Zhu, K., Operator theory in function spaces. Mathematical Surveys and Monographs, 138, American Mathematical Society, Providence, RI, 2007. http://dx.doi.Org/!0.1090/surv/138 Google Scholar