Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tijs, S. H.
and
Borwein, J. M.
1980.
Some Generalizations of Carathéodory′s Theorem Via Barycentres, with Application to Mathematical Programming.
Canadian Mathematical Bulletin,
Vol. 23,
Issue. 3,
p.
339.


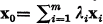 some
some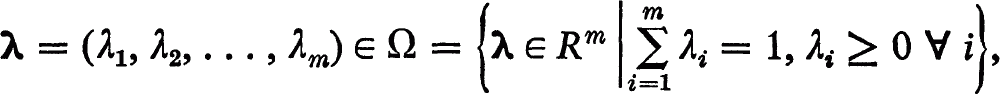
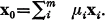 (See [5]). The authors of [2] have extended this result to include the case where
(See [5]). The authors of [2] have extended this result to include the case where 