Published online by Cambridge University Press: 20 November 2018
Let 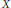 $X$ and
$X$ and  $Y$ be Banach spaces isomorphic to complemented subspaces of each other with supplements
$Y$ be Banach spaces isomorphic to complemented subspaces of each other with supplements 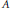 $A$ and
$A$ and  $B$. In 1996, W. T. Gowers solved the Schroeder–Bernstein (or Cantor–Bernstein) problem for Banach spaces by showing that
$B$. In 1996, W. T. Gowers solved the Schroeder–Bernstein (or Cantor–Bernstein) problem for Banach spaces by showing that 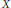 $X$ is not necessarily isomorphic to
$X$ is not necessarily isomorphic to  $Y$. In this paper, we obtain a necessary and sufficient condition on the sextuples
$Y$. In this paper, we obtain a necessary and sufficient condition on the sextuples 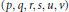 $\left( p,\,q,\,r,\,s,\,u,\,v \right)$ in
$\left( p,\,q,\,r,\,s,\,u,\,v \right)$ in 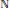 $\mathbb{N}$ with
$\mathbb{N}$ with 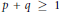 $p\,+\,q\,\ge \,1$,
$p\,+\,q\,\ge \,1$, 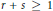 $r+s\ge 1$ and
$r+s\ge 1$ and 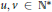 $u,\,v\,\in \,{{\mathbb{N}}^{*}}$, to provide that
$u,\,v\,\in \,{{\mathbb{N}}^{*}}$, to provide that 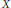 $X$ is isomorphic to
$X$ is isomorphic to  $Y$, whenever these spaces satisfy the following decomposition scheme
$Y$, whenever these spaces satisfy the following decomposition scheme
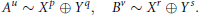 $${{A}^{u}}\,\sim \,{{X}^{p}}\,\oplus \,{{Y}^{q}},\,{{B}^{v}}\,\sim \,{{X}^{r}}\,\oplus \,{{Y}^{s}}.$$
$${{A}^{u}}\,\sim \,{{X}^{p}}\,\oplus \,{{Y}^{q}},\,{{B}^{v}}\,\sim \,{{X}^{r}}\,\oplus \,{{Y}^{s}}.$$
Namely, 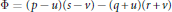 $\Phi \,=\,\left( p\,-\,u \right)\left( s\,-\,v \right)-\left( q\,+\,u \right)\left( r\,+\,v \right)$ is different from zero and
$\Phi \,=\,\left( p\,-\,u \right)\left( s\,-\,v \right)-\left( q\,+\,u \right)\left( r\,+\,v \right)$ is different from zero and 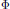 $\Phi $ divides
$\Phi $ divides 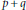 $p\,+\,q$ and
$p\,+\,q$ and 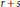 $r\,+\,s$. These sextuples are called Cantor–Bernstein sextuples for Banach spaces. The simplest case
$r\,+\,s$. These sextuples are called Cantor–Bernstein sextuples for Banach spaces. The simplest case 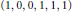 $\left( 1,0,0,1,1,1 \right)$ indicates the well-known Pełczyński's decomposition method in Banach space. On the other hand, by interchanging some Banach spaces in the above decomposition scheme, refinements of the Schroeder– Bernstein problem become evident.
$\left( 1,0,0,1,1,1 \right)$ indicates the well-known Pełczyński's decomposition method in Banach space. On the other hand, by interchanging some Banach spaces in the above decomposition scheme, refinements of the Schroeder– Bernstein problem become evident.