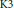 $\text{K}3$ Surfaces with Picard Number Two
$\text{K}3$ Surfaces with Picard Number TwoPublished online by Cambridge University Press: 20 November 2018
Let 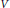 $V$ be an algebraic
$V$ be an algebraic 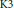 $\text{K}3$ surface defined over a number field
$\text{K}3$ surface defined over a number field 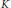 $K$. Suppose
$K$. Suppose 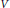 $V$ has Picard number two and an infinite group of automorphisms
$V$ has Picard number two and an infinite group of automorphisms 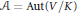 $\mathcal{A}\,=\,\text{Aut(}V/K\text{)}$. In this paper, we introduce the notion of a vector height
$\mathcal{A}\,=\,\text{Aut(}V/K\text{)}$. In this paper, we introduce the notion of a vector height 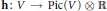 $\mathbf{h}:\,V\,\to \,\text{Pic(}V\text{)}\,\otimes \,\mathbb{R}$ and show the existence of a canonical vector height
$\mathbf{h}:\,V\,\to \,\text{Pic(}V\text{)}\,\otimes \,\mathbb{R}$ and show the existence of a canonical vector height 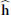 $\mathbf{\hat{h}}$ with the following properties:
$\mathbf{\hat{h}}$ with the following properties:
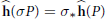 $$\widehat{\mathbf{h}}\,\left( \sigma P \right)\,=\,{{\sigma }_{*}}\widehat{\mathbf{h}}\left( P \right)$$
$$\widehat{\mathbf{h}}\,\left( \sigma P \right)\,=\,{{\sigma }_{*}}\widehat{\mathbf{h}}\left( P \right)$$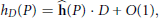 $${{h}_{D}}(P)\,=\,\mathbf{\hat{h}}(P)\,\cdot \,D\,+\,O(1),$$
$${{h}_{D}}(P)\,=\,\mathbf{\hat{h}}(P)\,\cdot \,D\,+\,O(1),$$
where 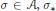 $\sigma \,\in \,\mathcal{A},\,{{\sigma }_{*}}$ is the pushforward of
$\sigma \,\in \,\mathcal{A},\,{{\sigma }_{*}}$ is the pushforward of 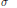 $\sigma $ (the pullback of
$\sigma $ (the pullback of 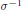 ${{\sigma }^{-1}}$), and
${{\sigma }^{-1}}$), and 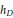 ${{h}_{D}}$ is a Weil height associated to the divisor
${{h}_{D}}$ is a Weil height associated to the divisor 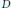 $D$. The bounded function implied by the
$D$. The bounded function implied by the 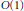 $O(1)$ does not depend on
$O(1)$ does not depend on  $P$. This allows us to attack some arithmetic problems. For example, we show that the number of rational points with bounded logarithmic height in an
$P$. This allows us to attack some arithmetic problems. For example, we show that the number of rational points with bounded logarithmic height in an 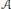 $\mathcal{A}$-orbit satisfies
$\mathcal{A}$-orbit satisfies
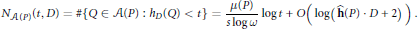 $${{N}_{\mathcal{A}(P)}}(t,\,D)\,=\,\#\{Q\,\in \,\mathcal{A}(P)\,:\,{{h}_{D}}(Q)\,<\,t\}\,=\,\frac{\mu (P)}{s\,\log \,\omega }\,\log t\,+\,O\left( \log \left( \mathbf{\hat{h}}(P)\,\cdot \,D\,+\,2 \right) \right).$$
$${{N}_{\mathcal{A}(P)}}(t,\,D)\,=\,\#\{Q\,\in \,\mathcal{A}(P)\,:\,{{h}_{D}}(Q)\,<\,t\}\,=\,\frac{\mu (P)}{s\,\log \,\omega }\,\log t\,+\,O\left( \log \left( \mathbf{\hat{h}}(P)\,\cdot \,D\,+\,2 \right) \right).$$
Here, 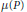 $\mu (P)$ is a nonnegative integer,
$\mu (P)$ is a nonnegative integer, 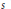 $s$ is a positive integer, and
$s$ is a positive integer, and  $\omega $ is a real quadratic fundamental unit.
$\omega $ is a real quadratic fundamental unit.